Syarat Dan Posisi Titik Berat Kesetimbangan Benda Tegar Dan Pembahasan Soal

Pembahasan gerak benda, baik translasi maupun rotasi, tidak lengkap tanpa membahas mengenai kesetimbangan benda tegar. Bagaimanakah benda dikatakan setimbang?

Kesetimbangan yaitu suatu keadaan kondisi benda dengan resultan gaya dan resultan momen gaya sama dengan nol dan jumlah torsi terhadap sembarang titik pada benda sama dengan nol.

Contents hide

1 Syarat Kesetimbangan Benda

2 Posisi Titik Kesetimbangan (Titik Berat)

2.1 a. Benda Homogen Teratur

2.2 b. Benda Gabungan Benda-Benda Homogen Teratur

3 Jenis-Jenis Kesetimbangan

3.1 1. Kesetimbangan Stabil

3.2 2. Kesetimbangan Labil

3.3 3. Kesetimbangan Netral (Indiferen)

3.4 Contoh Soal !

3.5 Baca postingan selanjutnya:

Syarat Kesetimbangan Benda

Sebuah benda dikatakan mengalami kesetimbangan (seimbang) secara translasi jika benda tersebut diam atau bergerak beraturan. Selain itu, benda dikatakan seimbang secara rotasi jika benda tersebut tidak berputar atau berputar dengan kecepatan sudut tetap. Secara lebih rinci, sebuah benda dikatakan setimbang jika memenuhi syarat-syarat. Syarat-syarat suatu benda dikatakan setimbang secara translasi yaitu resultan gaya yang bekerja pada benda itu bernilai nol. Dalam tinjauan vektor, jumlah komponen gaya harus bernilai nol, syarat ini dapat dirumuskan:

∑F = 0

∑F_x = 0

∑F_y = 0

∑F_z = 0

Sementara itu, syarat kesetimbangan untuk gerak rotasi yaitu nilai nol pada resultan torsi yang bekerja pada benda. Riimusan yang mewakili pengertian ini yaitu:

∑τ = 0

∑τ _kiri =∑τ _kanan

Kesetimbangan benda sangat diperlukan dalam permainan akrobat seperti . Sebelum melakukan atraksi, perhitungan kesetimbangan dan letak titik berat para pemain harus diperhitungkan.

Posisi Titik Kesetimbangan (Titik Berat)

Sebuah benda yang memenuhi syarat-syarat benda setimbang akan mempunyai suatu titik yang menjadi titik kesetimbangan benda itu. Titik ini biasa disebut titik berat. Pengertian titik berat yaitu titik tangkap resultan semua gaya yang bekerja pada benda. Pada benda-benda berukuran kecil, titik berat benda akan berimpit dengan pusat massa. Pusat massa merupakan tempat massa benda yang seakan-akan terkumpul (terpusat). Titik berat benda bergantung pada bentuk benda.

Letak titik berat berbagai jenis benda sebagai berikut.

a. Benda Homogen Teratur

Contoh benda homogen teratur sebagai berikut.

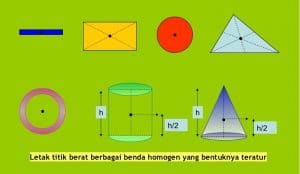
Titik berat untuk model benda ini terletak di tengah-tengah.

b. Benda Gabungan Benda-Benda Homogen Teratur

1) Dua Dimensi

Rumusan titik berat atau pusat gravitasi (x_pg, y_pg).

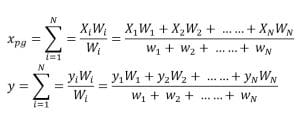
Keterangan:
X _{1,2,3, … N} = titik berat pada sumbu X benda 1,2,3,…N
Y _{1,2,3, … N} = titik berat pada sumbu Y benda 1,2,3,… N
W _{1,2,3,… N} = berat benda 1,2,3,… N

2) Tiga Dimensi

Titik berat atau titik pusat gravitasi dirumuskan sebagai berikut.

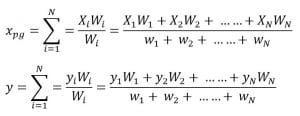
Jenis-Jenis Kesetimbangan

1. Kesetimbangan Stabil

Kesetimbangan ini bersifat mantap. Jika gangguan yang diberikan ke benda ini dihilangkan, benda akan kembaii ke posisi semula.Titik berat benda pada keadaan awal terletak di bawah.

2. Kesetimbangan Labil

Kesetimbangan ini bersifat tidak tetap. Jika gangguan yang diberikan kepada benda ini dihilangkan, benda tidak kembaii ke posisi semula. Titik berat benda pada keadaan awal terletak di atas.

3. Kesetimbangan Netral (Indiferen)

Kesetimbangan ini menghasilkan keadaan benda di antara kesetimbangan stabil dan netral. Hal ini disebabkan titik berat terletak segaris.

Contoh Soal !

Sebuah balok dengan massa 50 kg digantung pada dua utas tali yang bersambungan. Jika percepatan gravitasi 9,8 m/s2, tentukan besartegangan tali horizontalnya!

Penyelesaian:

Diketahui :
m = 50 kg
g = 9,8 m/s²

Ditanyakan : T _horizontal

Jawab:

∑F = 0
T sin 45° – w=0
T sin 45° = w

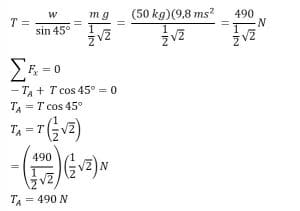
Tegangan tali horizontalnya 490 N.

Demikian penjelasan yang bisa kami sampaikan tentang Syarat Dan Posisi Titik Berat Kesetimbangan Benda Tegar Dan Pembahasan Soal. Semoga postingan ini bermanfaat bagi pembaca dan bisa dijadikan sumber literatur untuk mengerjakan tugas. Sampai jumpa pada postingan selanjutnya.