Rumus Segitiga – Segitiga adalah? Apa pengertian segitiga yang tepat? Apa rumus luas dan keliling segitiga? Sebutkan sifat-sifat segitiga! Apa saja jenis jenis segitiga?
Baca Juga : Rumus Persegi Panjang
Agar lebih memahaminya, kali ini kita akan membahas tentang pengertian segitiga, ciri sifat, gambar, rumus, contoh soal segitiga dan jawabannya secara lengkap.
Pengertian Segitiga
Segitiga atau segi tiga adalah bangun datar dua dimensi yang dibentuk oleh tiga sisi berupa garis lurus dan memiliki tiga sudut. Selain memiliki 3 sisi atau rusuk dan sudut, sifat yang dimiliki segitiga memiliki besar sudut 180°.
Jenis-Jenis Segitiga
Menurut panjang sisinya, terdapat 3 jenis segitiga yaitu:
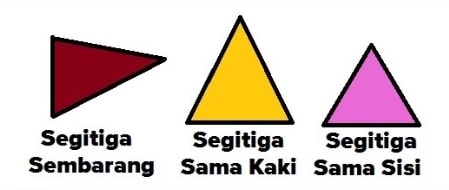
- Segitiga sama sisi (bahasa Inggris: equilateral triangle) adalah segitiga yang ketiga sisinya sama panjang dan semua sudutnya sama besar yaitu 60°.
- Segitiga sama kaki (bahasa Inggris: isoceles triangle) adalah segitiga yang dua dari tiga sisinya sama panjang dan memiliki dua sudut yang sama besar.
- Segitiga sembarang (bahasa Inggris: scalene triangle) adalah segitiga yang ketiga sisi memiliki panjang dan besar semua sudutnya berbeda.
Menurut besar sudut terbesarnya, segitiga dibagi menjadi 3 jenis yaitu:

- Segitiga siku-siku (bahasa Inggris: right triangle) adalah segitiga yang salah satu besar sudutnya sama dengan 90. Sisi di depan sudut 90° disebut hipotenusa atau sisi miring.
- Segitiga lancip (bahasa Inggris: acute triangle) adalah segitiga yang besar semua sudut < 90°
- Segitiga tumpul (bahasa Inggris: obtuse triangle) adalah segitiga yang besar salah satu sudutnya > 90°.
Sifat Segitiga
Berikut ini sifat-sifat bangun segitiga, diantaranya yaitu:
Sifat segitiga sama sisi, diantaranya yaitu:
- Memiliki tiga sisi yang sama panjang.
- Memiliki sudut yang sama besar, yakni masing-masing 60°.
- Memiliki tiga sumbu simetri yang berpotongan tepat di satu titik.
- Dapat ditempatkan pada bingkainya tepat dalam enam cara.
Sifat segitiga sama kaki, diantaranya yaitu:
- Dua buah sisinya sama panjang.
- Memiliki dua buah sudut sama besar.
- Memiliki sebuah sumbu simetri.
- Dapat ditempatkan pada bingkainya tepat dalam dua cara.
Sifat segitiga sebarang, diantaranya:
- Panjang ketiga sisinya berlainan.
- Besar ketiga sudutnya tidak sama.
Rumus Segitiga
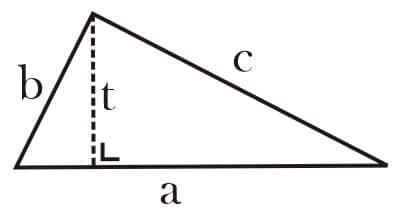
Keterangan:
a = alas
t = tinggi, tinggi segitiga membentuk sudut 90° terhadap alasnya.
b, c = sisi lain segitiga
Luas Segitiga
L = 1/2.alas.tinggi
Keliling Segitiga
K = sisi x sisi x sisi
Tinggi Segitiga
t = (2 × Luas) : a
Alas Segitiga
a = (2 × Luas) : t
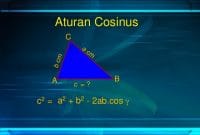
Teorema heron, teorema ini biasnya digunakan untuk mencari luas segitiga sembarang a,b,c adalah ketiga sisi segitiga.
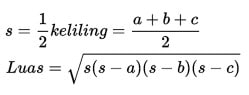
Rumus yang digunakan untuk mencari luas dan keliling segitiga sama sisi yang bersisi a dapat menggunakan rumus berikut ini:
Baca Juga : Rumus Persegi
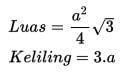
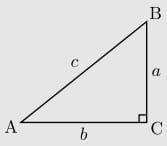
Rumus Pythagoras
Dalil phytagoras hanya berlaku pada segitiga siku-siku. pythagoras menyatakan bahwa: c² = a²+b²
Contoh Soal Segitiga
Berikut ini contoh soal bangun segitiga dan pembahasannya:
1. Perhatikan gambar dibawah ini!
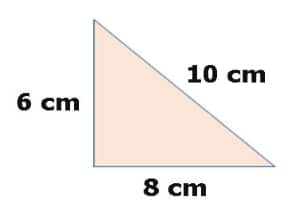
Berapa luas dan keliling segitiga tersebut!
Pembahasan:
Diketahui:
Panjang sisi segitiga:
a = 6 cm (alas) , b = 8 cm (tinggi), dan c = 10 cm (sisi miring)
Ditanya: keliling dan luas segitiga?
a. Keliling Segitiga
K = sisi a + sisi b + sisi c
K = 6 cm + 8 cm + 10 cm
K = 24 cm
b. Luas Segitiga
L = 1/2 x a x t
L = 1/2 x 6 x 8
L = 24 cm
2. Luas segitiga 75 cm². Jika tingginya 15 cm, berapakah panjang alas segitiga tersebut?
Pembahasan:
Diketahui:
luas segitiga = 75 cm²
tinggi = 15 cm
Ditanya: panjang alas?
L = 1/2 x a x t
75 = 1/2 x a x 15
t = 75 x 2 : 15
t = 10 cm
3. Selembar kertas berbentuk segitiga sama sisi dengan keliling 120 cm, maka berapakah panjang sisi-sisinya?
Pembahasan:
Diketahui:
Keliling segitiga sama sisi = 120 cm
Ditanya: panjang sisi?
Jawab:
K = 3 x panjang sisi
120 = 3 x panjang sisi
Panjang sisi = 120 : 3
Panjang sisi = 40 cm
4. Diketahui panjang sisi sebuah segitiga sama sisi 12 cm, berapakah keliling segitiga sama sisi tersebut?
Pembahasan:
Diketahui:
Panjang sisi = 12 cm
Ditanya: Keliling?
Jawab:
K = 3 x panjang sisi
K = 3 x 12 cm
K = 36 cm
Baca Juga : Macam-Macam Bangun Datar
5. Sebuah taman bunga berbentuk segitiga dengan ukuran 125 cm, 55 cm, dan 80 cm. Apabila taman tersebut dikelilingi pagar kawat 4 tingkat, maka berapa banyak kawat yang dibutuhkan?
Pembahasan:
Diketahui:
Ukuran segitiga = 125 cm, 55 cm, dan 80 cm
Pagar kawat = 4 tingkat
Ditanya: kawat yang dibutuhkan?
Jawab:
hitung keliling segitiga terlebih dahulu
K = sisi a + sisi b + sisi c
K = 145 cm + 55 cm + 100 cm
K = 300 cm = 3 meter
Kawat yang dibutuhkankan = K x 4
Kawat yang dibutuhkankan = 3 m x 4 = 12 m
6. Sebuah segitiga memiliki panjang alasnya 12 m dan tingginya 16 m, berapakah luasnya?
Pembahasan:
Diketahui:
panjang alas = 12 m
tinggi = 16 m
Ditanya: luas?
Jawab:
L = 1/2 x a x t
L = 1/2 x 12 x 16
L = 96 m²
Jadi, luas segitiga tersebut adalah 96 m²
7. Sebuah kolam berbentuk segitiga sama sisi dengan panjang sisinya 15 m. kolam tersebut akan dipagar bambu, dibutuhkan 5 bambu/m. Berapa banyak bambu yang dibutuhkan untuk mengelilingi kolam?
Pembahasan:
Diketahui:
panjang sisi segitiga = 15 cm
Bambu yang dibutuhkan per m² = 5
Ditanyakan: banyaknya bambu yang dibutuhkan?
Jawab:
hitung keliling segitiga terlebih dahulu:
K = 3 x sisi
K = 3 x 15 m
K = 45 meter
Kawat yang diperlukan = K x 5
Kawat yang diperlukan = 45 m x 5 = 225
8. Sebuah kolam ikan berbentuk segitiga sama sisi dengan panjang sisi 8 m. Apabila kolam tersebut akan dipagari kawat 5 tingkat disekelilingnya, maka berapa panjang kawat yang dibutuhkah?
Pembahasan:
Diketahui panjang sisi segitiga = 8 m
Pagar kawat = 5 tingkat
Ditanya: panjang kawat yang dibutuhkan?
Jawab:
hitung keliling segitiga terlebih dahulu:
K = 3 x sisi
K = 3 x 8 m
K = 24 meter
Kawat yang dibutuhkan = K x 5
Kawat yang dibutuhkan = 24 m x 5 = 120 meter
9. Sebuah kain berbentuk segitiga sama sisi dengan panjang sisinya 2,5 meter. Di sekeliling kain dihiasi manik berjarak 5 cm satu sama lain. Berapa banyak manik pada kain tersebut?
Pembahasan:
Diketahui:
panjang sisi segitiga = 2,5 m
Jarak mawar flanel = 5 cm
Ditanya: jumlah manik?
Jawab:
hitung keliling kain:
K = 3 x panjang sisi
K = 3 x 2,5 m
Keliling kain = 7,5 m = 750 cm
Baca Juga : Rumus Jajar Genjang
Banyak manik = keliling kebun : jarak manik
Banyak manik = 450 : 5
Banyak manik = 150
10. Perhatikan gambar berikut ini!
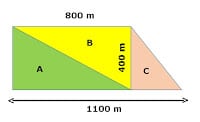
Paman memiliki kebun berbentuk seperti gambar diatas, pada daerah A akan ditanami sawi, daerah B akan ditanami kangkung, dan daerah C akan ditanami bayam. Hitunglah luas daerah yang ditanami sawi dan bayam!
Pembahasan:
Diketahui panjang alas bangun A dan bangun B = 400 m, tinggi 800 m
Panjang alas bangun C = 1.100 m – 800 m = 300 m, tinggi = 400 m
Ditanyakan daerah yang ditanami sawi dan bayam (a dan c) ?
Jawab:
L a = 1/2 x a x t
L a = 1/2 x 400 x 800
L a = 160.000 m²
L c = 1/2 x a x t
L c = 1/2 x 300 x 400
L c = 60.000 m²
Jadi, luas daerah yang ditanami sawi 160.000 m² dan luas daerah yang ditanami bayam 60.000 m²
11. Kebun kakek berbentuk segitiga dengan panjang tiap sisi adalah 8 m, 10 m, dan 12 m. Di sekeliling kebun tersebut akan dipasang pagar dengan biaya Rp 80.000,00/meter. Berapakah biaya yang diperlukan untuk pemasangan pagar kebun kakek?
Pembahasan:
Diketahui:
panjang tiap sisi = 8 m, 10 m, dan 12 m
Biaya = Rp 80.000,00/meter
Ditanya: total biaya yang diperlukan?
Jawab:
Untuk menghitung biaya yang diperlukan, maka kita harus menghitug keliling segitiga.
K = sisi a + sisi b + sisi c
K = 8 m + 10 m + 12 m
K = 30 meter
Biaya yang diperlukan = K x biaya per meter
Biaya yang diperlukan = 30 meter x Rp 80.000,00/meter
Biaya yang diperlukan = Rp 2.400.000,00
12. Diketahui segitiga ABC siku-siku di B. Jika Luasnya 270 cm² dan panjang AB 15 cm, hitunglah keliling segitiga tersebut!
Pembahasan:
Diketahui:
luas segitiga = 270 cm²
panjang AB (tinggi) = 15 cm
Ditanya: keliling?
Jawab:
Untuk menghitung keliling segitiga, kita harus mencari panjang alasnya (BC) dan sisi miring (AC).
L = 1/2 x a x t
270 = 1/2 x BC x 16
BC = 270 x 2 : 15
BC = 36 cm
Panjang alas (BC) = 36 cm
Sekarang cari sisi miring dengan cara dengan Rumus Pythagoras:
AC² = AB² + BC²
AC² = 15² + 36²
AC² = 1.521
AC = √1.521
AC = 39 cm
Panjang sisi miring (AC) = 39 cm
K segitiga siku-siku ABC = AB + BC + AC
K segitiga siku-siku ABC = 15 cm + 36 cm + 39 cm
K segitiga siku-siku ABC = 90 cm
Baca Juga : Pengertian Bangun Ruang
13. Sebuah segitiga siku-siku dengan luas 240 cm² dan tinggi 16 cm, hitunglah keliling segitiga siku-siku tersebut!
Pembahasan:
Diketahui:
luas segitiga = 240 cm²
tinggi : 16 cm
Ditanyakan keliling?
Jawab:
Untuk menghitung keliling segitiga, kita harus mencari panjang alasnya dan sisi miring.
L = 1/2 x a x t
240 = 1/2 x a x 16
a = 240 x 2 : 16
a = 30 cm
Panjang alas = 30 cm
Sekarang kita harus mencari sisi miring dengan cara menggunakan Rumus Pythagoras
c² = a² + b²
c² = 16² + 30²
c² = 1.156
c = √1.156
c = 34
Panjang sisi miring = 34 cm
K segitiga siku-siku = tinggi + alas + sisi miring
K segitiga siku-siku = 16 cm + 30 cm + 34 cm
K segitiga siku-siku = 80 cm
Jadi keliling segitiga siku-siku adalah 80 cm
14. Hitunglah luas segitiga sama kaki dengan panjang sisi yang sama 50 cm dan tingginya 14 cm!
Pembahasan:
Diketahui:
panjang sisi (sisi miring) = 50 cm
tinggi = 14 cm
Ditanya: luas?
Jawab:
Untuk menghitung luas segitiga, kita harus mencari panjang alasnya dengan cara menggunakan Rumus Pythagoras
c² = a² + b²
50² = 14² + b²
b² = 50² – 14²
b² = 2.500 – 196
b² = 2.304
b = √2.304
b = 48 cm
Panjang alas = 48 cm
Panjang alas segitiga sama kaki = 2 x 48 = 96 cm
Jadi, luas segitiga sama kaki tersebut yaitu:
L = 1/2 x a x t
L = 1/2 x 96 x 14
L = 672 cm²
15. Perhatikan gambar dibawah ini!
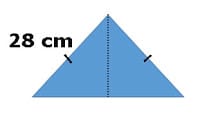
Jika keliling bangun di atas 90 cm, maka berapa panjang alas segitiga tersebut?
Pembahasan:
Diketahui:
keliling = 90 cm
panjang sisi = 28 cm
Ditanya: panjang alasnya?
Jawab:
K = sisi a + sisi b + sisi c
90 = 28 cm + 28 cm + sisi alas
Sisi alas = 90 cm – (28 cm + 28 cm)
Sisi alas = 34 cm
Baca Juga : Rumus Tabung
Demikian artikel pembahasan tentang pengertian segitiga, ciri sifat, gambar, rumus, contoh soal segitiga dan jawabannya secara lengkap. Semoga bermanfaat