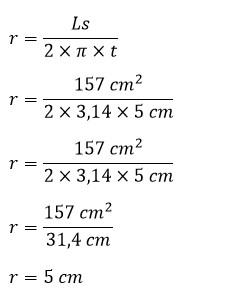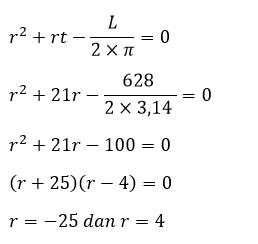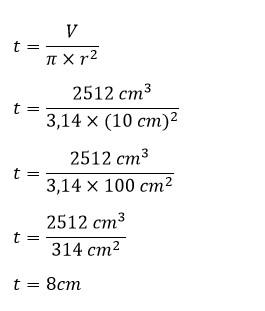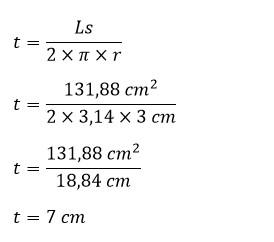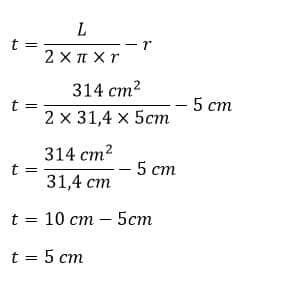Rumus Tabung : Volume, Luas Permukaan, Keliling, Tinggi dan Contoh Soal Tabung – Dalam matematika kita mempelajari tentang bangun ruang. Bangun ruang adalah sebuah penamaan atau sebutan untuk beberapa bangun-bangun yang berbentuk tiga dimensi atau bangun yang memiliki ruang yang dibatasi oleh sisi-sisinya.
Ada 7 macam jenis bangun ruang, salah satunya adalah tabung. Apa itu bangun tabung? agar lebih memahaminya, kali ini kita akan membahas rumus tabung mulai dari rumus volume tabung, rumus keliling tabung, menghitung luas tabung hingga mengetahui rumus tabung tanpa tutup, berikut selengkapnya:
Pengertian Bangun Tabung
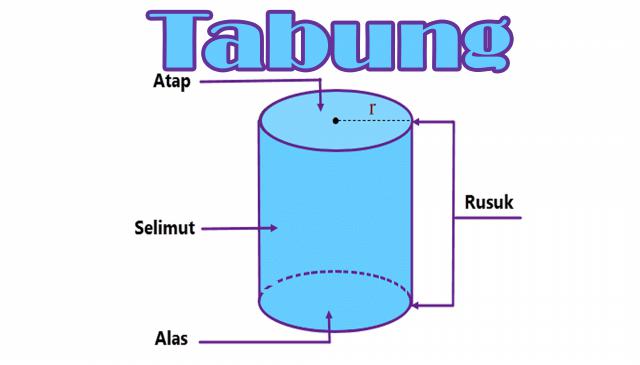
Bangun Tabung adalah sebuah bangun ruang tiga dimensi yang memiliki tutup dan alas yang berbentuk sebuah lingkaran dengan ukuran yang sama dengan di selimuti oleh persegi panjang. Tabung juga disebut dengan silinder.
Baca Juga : Rumus Bola dan Contoh Soalnya
Ada banyak benda berbentuk tabung yang kita temui di kehidupan sehari-hari seperti gelas, kaleng susu, drum, botol, seruling dan lain sebagainya. Berikut gambar bangunan tabung:
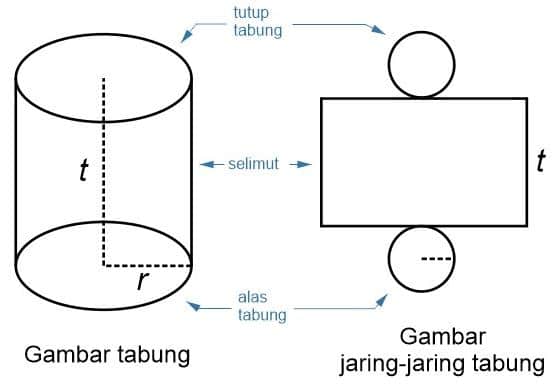
Sifat Sifat Bangun Tabung
Ciri ciri tabung diantaranya yaitu:
- Memiliki 2 (dua) buah rusuk lengkung.
- Memiliki alas dan tutup berbentuk lingkaran yang masing-masing sama besar.
- Memiliki 3 (tiga) buah sisi diantaranya dua buah sisi berbentuk lingkaran dan satu sisi selimut berbentuk persegi panjang.
- Tidak memiliki titik sudut
Jenis-Jenis Tabung
Ada 2 jenis tabung yaitu
Tabung Tertutup
Tabung Tertutup adalah sebuah tabung yang seluruh bidang dan sisi – sisinya tertutup.
Tabung Terbuka
Tabung Terbuka adalah sebuah tabung yang salah satu sisi alasnya atau sisi atapnya terbuka dan bahkan keduanya antara sisi alas dan sisi atapnya juga terbuka.
Rumus Menghitung Luas dan Volume Tabung
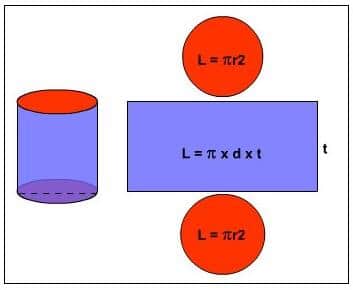
Keterangan:
V = Volume tabung(cm3)
π = 22/7 atau 3,14
r = Jari – jari /setengah diameter (cm)
t = Tinggi (cm)
Baca Juga: Rumus Balok dan Contoh Soalnya
Rumus Luas Permukaan Tabung
Luas permukaan tabung adalah suatu luas dari beberapa jumlah sisi yang dimiliki tabung. Jumlah sisi suatu tabung sama dengan bidang pembentuk tabung. Bidang pembentuknya terdiri dari dua buah lingkaran yang menjadi alas dan tutupnya, dan satu buah selimut tabung yang berbentuk persegi panjang. Luas permukaan ini memiliki pengaruh terhadap besar dan kecilnya suatu tabung.
Untuk rumus luas permukaan tabung bisa dicari menggunakan sebuah jaring-jaring tabung. Jaring-jaring tabung tersebut terdiri dari
Tutup dan atas tabung yang berbentuk lingkaran dengan besar jari-jari (r), sehingga rumus luas lingkaran = 2πr². Untuk jari-jarinya bisa menggunakan π= 22/7 atau 3,14.
Bagian lengkungannya berbentuk persegi pajang dengan panjang tabung memiliki rumus keliling alas tabung yaitu 2πr serta bagian lebar tabung yang memiliki rumus luas 2πrt.
Berdasarkan ulasan rumus luas tabung tersebut, maka dapat disimpulkan:
Rumus luas tutup serta alas tabungnya yaitu πr² + πr² = 2πr²
Rumus luas selimut tabung yaitu p (keliling alas) x l (tinggi tabung) = 2πr x t = 2πrt
Maka, rumus luas permukaan tabung yaitu = Luas tutup + alas + selimut tabung = 2πr²+2πrt = 2πr(r+t)
Rumus Luas Permukaan Tabung Tanpa Tutup
Luas permukaan tabung tanpa tutup adalah suatu luas permukaan yang hampir sama dengan luas permukaan tabung, hanya berbeda pada segi tutupnya saja, luas permukaan tanpa tutup tabung ini tidak ada tutupnya. Karena tidak memiliki tutup, maka luas sisi tutup tabung yang berupa lingkaran tersebut tidak dihitung.
Rumus luas tutup tabung : 2πr
Rumus luas alas tabung : 2πr
Rumus luas selimut tabung : 2πr²t
Karena tanpa tutup, maka rumus luas permukaan tabung tanpa tutup bisa disimpulkan sebagai berikut:
Luas tabung tanpa tutup = π x r2 + 2 x π x r x t = π x r (r + 2t)
Baca Juga : Rumus Kubus dan Contoh Soalnya
Rumus Volume Tabung
Rumus volume tabung adalah perkalian antara tinggi dengan luas alas tabung. Bangun tabung memiliki sebuah alas dan tutup yang berbentuk lingkaran, untuk itu untuk menghitung volumenya cukup mengalikan tinggi dengan luas alasnya saja. Berikut rumus volume tabung:
Volume Tabung = πr²t
Rumus Keliling Alas Tabung
Karena alas tabung berbentuk lingkaran, maka rumus keliling alas tabung yaitu:
Keliling alas = 2πr
Rumus Luas Jaring-Jaring Tabung
L = alas x tinggi = a x t
Rumus Gabungan Kerucut
Selain rumus-rumus diatas ada juga rumus gabungan antara tabung dengan bangun lainnya seperti gabungan tabung dan kerucut, gabungan tabung dan setengah lingkaran, serta gabungan tabung dan lingkaran . Berikut ini rumus gabungannya:
Rumus gabungan kerucut dan tabung
Rumus volume gabungan tabung dan kerucut yaitu ( π.r².t )+( 1/3.π.r².t )
Rumus luas gabungan tabung dan kerucut yaitu (π.r²)+(2.π.r.t)+(π.r.s)
Rumus gabungan tabung dan setengah bola
Rumus volume gabungan tabung dan setengah bola yaitu π.r².t+2/3. π.r3
Rumus luas gabungan tabung dan setengah bola (π.r²)+(2.π.r.t)+(½.4.n.r²) = (3.π.r²)+(2. π .r.t)
Rumus gabungan tabung dan bola
Rumus volume gabungan tabung dan bola yaitu (π.r².t)+(4/3. π.r3)
Rumus luas gabungan tabung dan bola yaitu (2. π.r²)+(4. π.r²) = π.r²
Baca Juga : Rumus Prisma dan Contoh Soalnya
Contoh Soal Tabung dan Pembahasannya
Contoh Soal Volume Tabung
Contoh Soal Luas Permukaan Tabung
Baca Juga : Jaring-Jaring Balok
Contoh Soal Luas Selimut Tabung
Apabila ada sebuah tabung yang diketahui memiliki jari- jari yaitu 18 cm. Carilah dan hitunglah keliling alas tabung tersebut:
Penyelesaian :
Diketahui :
r = 18 cm
Ditanya : K = …?
Jawab :
K = 2 x π x r
K = 2 x 22/7 x 18
K = 792 / 7
K = 113.14 cm
Maka, keliling alas tabung tersebut adalah 113.14 cm
[/su_spoiler]Contoh Soal Luas Permukaan Tabung Tanpa Tutup
Diketahui sebuah tabung berdiameter 20 cm dengan tinggi tabung adalah 24 cm. Berapakah luas permukaan tabung tanpa tutup tersebut?
Jawab:
Rumus luas permukaan tabung tanpa tutup = π x r (r + 2t)
= 3,14 x 10 x (10 x 2 x 24)
= 3,14 x 10 x (10 x 48)
= 3,14 x 10 x 480
= 15.072 cm2
Jadi, luas permukaan tabung tanpa tutup adalah 15.072 cm2
[/su_spoiler]Baca Juga : Rumus Limas dan Contoh Soalnya
Contoh Soal Menghitung Jari-Jari Tabung Jika Diketahui Volume Tabung
Hitunglah jari-jari tabung yang memiliki tinggi 8 cm dan volume 2512 cm³!
Diketahui:
t = 8 cm
V = 2512 cm³
Ditanya:
Jari-jari tabung (r)
Pembahasan:
Jadi, jari-jari tabung adalah 10 cm.
Contoh Soal Menghitung Jari-Jari Tabung Jika Diketahui Luas Selimut
Hitunglah jari-jari tabung yang mempunyai tinggi 5 cm dan luas selimut 157 cm²!
Diketahui:
t = 5 cm
Ls = 157 cm
Ditanya:
Jari-jari tabung (r)
Pembahasan:
Jadi, jari-jari tabung adalah 5 cm.
Contoh Soal Menghitung Jari-Jari Tabung Jika Diketahui Luas Permukaan
Hitunglah jari-jari tabung yang mempunyai tinggi 21 cm dan luas permukaan 628 cm²!
Diketahui:
t = 21 cm
L = 628 cm²
Ditanya:
Jari-jari tabung (r)
Penyelesaian:
Jari-jari tabung memenuhi persamaan berikut
Dari hasil faktor persamaan dapat diuji
r = -25 cm tidak memenuhi syarat, karena hasil luas permukaan akan bernilai negatif atau tidak sama 628 cm².
r = 4 cm memenuhi syarat, karena hasil hasil luas permukaan bernilai 628 cm².
Jadi, jari-jari tabung tersebut adalah 4 cm.
Baca Juga : Rumus Lingkaran dan Contoh Soalnya
Contoh Soal Menghitung Tinggi Tabung Jika Diketahui Volume
Hitunglah tinggi tabung yang mempunyai jari-jari 10 cm dengan volume 2512 cm³!
Diketahui:
r = 10 cm
V = 2512 cm³
Ditanya:
Tinggi tabung (t)
Penyelesaian:
Jadi, tinggi tabung 8 cm.
Contoh Soal Menghitung Tinggi Tabung Jika Diketahui Luas Selimut
Hitunglah tinggi tabung yang mempunyai jari-jari 3 cm dengan luas selimut 131,88 cm²!
Diketahui:
r = 3 cm
Ls = 131,88 cm²
Ditanya:
Tinggi tabung (t)
Penyelesaian:
Baca Juga : Bangun Datar
Contoh Soal Menghitung Tinggi Tabung Jika Diketahui Luas Permukaan
Hitunglah tinggi tabung yang mempunyai jari-jari 5 cm dengan luas permukaan 314 cm²
Diketahui:
r = 5 cm
L = 314 cm²
Ditanya:
Tinggi tabung (t)
Penyelesaian:
Contoh Soal Volume dan Luas Permukaan Gabungan Tabung dan Setengah Lingkaran
Tentukan volume dan luas permukaan.
Jawab:
Diketahui diameter tabung = diameter bola = 20 cm. Maka jari-jarinya = 20/2 = 10 cm
Volume bangun
= Volume tabung + volume setengah bola
= Pi x r² x t + 1/2 x 4/3 x Pi x r³
= 3,14 x 10 x 10 x 14 + 2/3 x 3,14 x 10 x 10 x 10
= 314 x 14 + 2/3 x 3.140
= 4.396 + 2.093,33
= 6.489,33
Luas Permukaan bangun
= Luas alas + Luas selimut tabung + Luas setengah bola
= Pi x r² + 2 x Pi x r x t + 1/2 x 4 x Pi x r²
= Pi x r x (r + 2t + 2r)
= Pi x r x (3r + 2t)
= 3,14 x 10 x (30 + 28)
= 3,14 x 10 x 58
= 1.821,2
Jadi, volume bangun = 6.489,33 cm3 dan Luas Permukaannya = 1.821,2 cm²
Demikian pembahasan rumus tabung dan contoh soalnya, semoga bermanfaat.