Rumus Luas Permukaan dan Volume Kubus – Kubus adalah bangun? Apa yang dimaksud dengan kubus? Apa itu kubus? Apa rumus rusuk dan keliling kubus? Apa rumus luas permukaan dan volume kubus? Apa saja unsur-unsur kubus? Sebutkan sifat-sifat kubus!
Baca Juga : Macam-Macam Bangun Ruang
Agar lebih memahaminya, kali ini kita akan membahas tentang pengertian kubus, sifat, unsur, rumus, jaring-jaring kubus, contoh soal kubus dan cara penyelesaiannya secara lengkap.
Pengertian Kubus
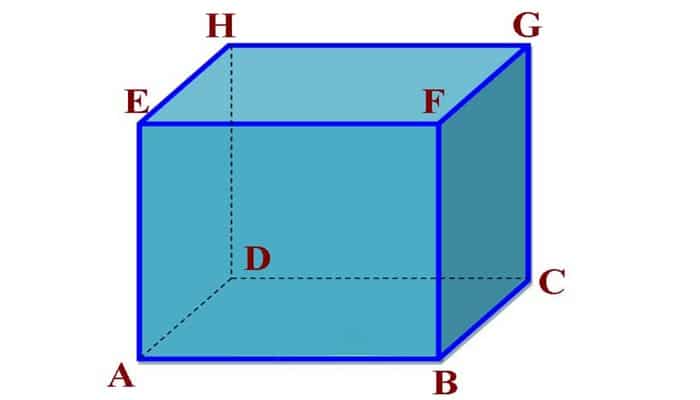
Kubus adalah bangun ruang tiga dimensi yang dibatasi oleh enam bidang kongruen berbentuk bujur sangkar atau persegi. Ciri-ciri kubus memiliki enam sisi yang berukuran sama (kongruen), duabelas rusuk, dan delapan titik sudut. Kubus juga disebut bidang enam beraturan, kubus juga merupakan bentuk khusus prisma segi empat. Contoh benda berbentuk bangun kubus yaitu dadu, kardus dan lain sebagainya.
Sifat-Sifat Kubus
Berikut ini sifat atau ciri-ciri bangun kubus, diantaranya:
- Memiliki 6 sisi yang kongruen.
- Memiliki 12 rusuk.
- Memiliki 8 titik sudut.
- Semua sisi kubus berbentuk persegi.
- Semua rusuk kubus beukuran sama panjang.
- Setiap diagonal bidang pada kubus memiliki ukuran yang sama panjang.
- Setiap diagonal ruang pada kubus memiliki ukuran yang sama panjang.
- Setiap bidang diagonal pada kubus memiliki bentuk persegi panjang.
Unsur-Unsur Kubus
Berikut ini unsur atau bagian bangun kubus, diantaranya yaitu:
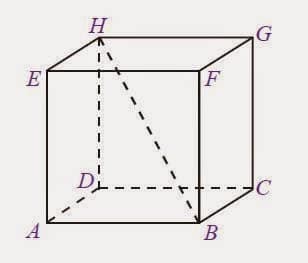
Sisi atau Bidang Kubus
Sisi atau bidang kubus adalah Bidang atau sisi yang membatasi Kubus. Kubus memiliki 6 sisi. Perhatikan gambar kubus diatas, yang merupakan sisi atau bidang kubus yaitu (ABCD), (EFGH), (ABFE), (DCGH), (BCGF), dan (ADHE).
Rusuk
Rusuk adalah garis potongan antar dua sisi bidang kubus dan terlihat seperti kerangka yang menyusun kubus. Kubus mnemiliki 12 rusuk. Perhatikan gambar kubus diatas, yang merupakan Rusuk yaitu AB, BC, CD, DA, AE, BF, CG, DH, EF, FG, GH, dan HE.
Titik Sudut
Titik Sudut adalah titik potongan antara dua atau 3 rusuk. Kubus memiliki 8 titik sudut. Perhatikan gambar kubus diatas, yang merupakan Titik Sudut yaitu A, B, C, D, E, E, F, G, dan H.
Diagonal Bidang atau Diagonal Sisi
Diagonal bidang atau diagonal sisi adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan pada setiap bidang atau sisi kubus. Kubus memiliki 12 diagonal sisi atau diagonal bidang. Sekarang coba perhatikan bidang ABEF pada gambar kubus ABCD.EFGH di bawah ini.
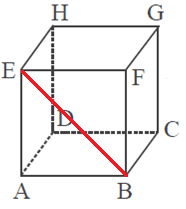
Yang merupakan diagonal bidang diantaranya : AF, BE, BG, CF, CH, DG, DE, AH, AC, BD, EG, dan HF. Diagonal bidang atau sisi dapat ditentukan dengan menggunakan teorema phytagoras. Sekarang perhatikan gambar kubus di bawah ini.
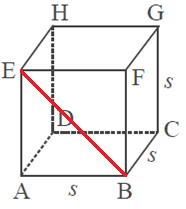
Bagaimana cara menghitung panjang diagonal bidang atau diagonal sisi pada kubus? Misalkan kubus ABCD.EFGH di atas memiliki rusuk s. Maka panjang BE dapat dihitung dengan menggunakan teorema phytagoras, di mana segitiga ABE siku-siku di A. Sehingga:
BE = √(AB² + AE²)
BE = √(s² + s²)
BE = √2s²
BE = s√2
Baca Juga : Rumus Tabung
Misalkan diagonal bidang kubus adalah b maka secara umum diagonal bidang kubus dapat dirumuskan:
b = s√2
Diagonal Ruang
Diagonal ruang adalah garis yang menghubungkan 2 titik sudut yang saling berhadapkan dalam satu ruang. Kubus memiliki 4 diagonal ruang. Perhatikan gambar kubus dibawah ini.
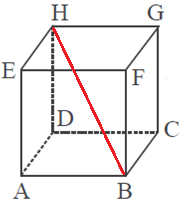
Yang merupakan diagonal ruang adalah AG , BH , CE , dan DF .
Bagaimana menghitung panjang diagonal ruang kubus? Sama seperti mencari diagonal bidang, untuk mencari diagonal ruang juga menggunakan teorema phyagoras. Sekarang perhatikan gambar di bawah ini.
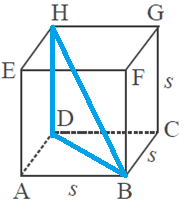
Misalkan kubus ABCD.EFGH di atas memiliki rusuk s. Maka panjang BH dapat dihitung dengan menggunakan teorema phytagoras. Tetapi sebelum itu harus cari panjang BD, di mana BD merupakan diagonal sisi. Sekarang perhatikan segitiga ABD siku-siku di A. Sehingga:
BD = s√2
Sekarang cari panjang BH dengan teorema phytagoras juga. Sekarang perhatikan segitiga BDH siku-siku di D. Sehingga:
BH = √(BD² + DH²)
BH = √(s√2)² + s²)
BH = √(2s² + s²)
BH = √(3s²)
BH = s√3
Misalkan diagonal ruang kubus adalah d, maka secara umum diagonal ruang kubus dapat dirumuskan:
d = s√3
Bidang Diagonal Kubus
Bidang diagonal suatu kubus adalah bidang yang dibatasi oleh dua rusuk dan dua diagonal bidang suatu kubus. Terdapat 6 Bidang diagonal pada Kubus. Perhatikan gambar dibawah ini:
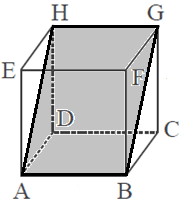
Bidang ABGH disebut bidang diagonal, selain itu yang merupakan bidang diagonal yaitu ACGE, AFGD, CDEF, BFHD, dan BEHC. Bagaimana menghitung luas bidang diagonal?
Untuk menghitung luas bidang diagonal dapat menggunakan rumus luas persegi panjang. Sekarang coba perhatikan kembali gambar kubus ABCD.EFGH di atas, jika rusuknya s, maka luas bidang ABGH yakni:
Luas ABGH = AB . BG
Luas ABGH = s . s√2
Luas ABGH = s√2
Jaring-Jaring Kubus
Jaring-Jaring adalah bidang datar yang berupa gabungan dari bangun datar yang membentuk sebuah bangun ruang seperti kubus, balok, limas dan lain sebagainya. Jaring-jaring bisa didapatkan dengan cara membagi sebuah bangun ruang dengan mengikuti rusuk-rusuknya.
Baca Juga : Rumus Kerucut
Jaring-jaring kubus terdiri dari 6 buah bangun datar persegi atau bujur sangkar. Berikut adalah Jaring-Jaring Kubus:

Keterangan:
A : Alas
T : Tutup
Rumus Kubus
Luas Permukaan Kubus
L : 6.S²
Volume Kubus
V : S3
Keliling Kubus
K : 12.S
Diagonal Bidang/sisi Kubus
Ds: S√2
Diagonal Bidang/sisi seluruhnya Kubus
Dss : 12. S√2
Diagonal Ruang Kubus
Dr : S√3
Diagonal Ruang Kubus
Drr : 4. S√3
Luas Bidang Diagonal Kubus
Bd : S2 √2
Luas Bidang Diagonal Kubus seluruhnya
Bdd: 6. S² √2
Keterangan:
S : rusuk atau sisi.
Contoh Soal Kubus
Berikut ini contoh soal kubus dan pembahasannya:
1. Sebuah Kubus memiliki panjang rusuk 8 cm. Tentukan:
a. Luas permukaan kubus.
b. Volume kubus.
c. Keliling kubus.
Pembahasan:
Diketahui : rusuk kubus (s) : 8 cm
Ditanya :
a. Luas permukaan (L)?
b. Volume (V)?
c. Keliling (K)?
Jawab :
a. Luas Permukaan
L : 6.S²
L : 6.S x S
L : 6. 8 x 8
L : 6. 64
L : 384 cm²
Baca Juga : Macam-Macam Bangun Datar
b. Volume Kubus
V : S3
V : s x s x s
V : 8 cm x 8 cm x 8 cm
V : 512 cm3
c. Keliling kubus
K : 12.S
K : 12.8
K : 96 cm
2. Sebuah kubus memiliki panjang rusuk 4 cm. Hitunglah:
a. Diagonal bidang.
b. Diagonal ruang.
c. Luas salah salah satu bidang diagonal.
Pembahasan:
Diketahui : Panjang rusuk (s) : 4 cm
Ditanya :
a. Diagonal bidang (Ds)
b. Diagonal ruang (Dr)
c. Luas salah salah satu bidang diagonal (Bd)
Jawab:
a. Diagonal bidang
Ds : S√2
Ds : 4√2
b. Diagonal ruang
Dr : S√3
Dr : 4√3
c. Luas salah salah satu bidang diagonal
Bd: S2 √2
Bd : (4 cm)² . √2
Bd : 16√2 cm²
3. Chyntia akan mengirimkan paket pada saudaranya berupa 125 souvenir yang akan dikemas dalam kotak berbentuk kubus kecil berukuran panjang 4 cm. Sebelum dikirim, souvenir tersebut dimasukkan dalam kardus besar berbentuk kubus hingga kardus terisi penuh. Berapakah ukuran panjang kotak kardus besar yang digunakan Chintya?
Pembahasan:
Diketahui :
Jumlah kotak souvenir : 125
Rusuk kotak souvenir : 4 cm
Ditanya: Panjang rusuk kotak besar(s)?
Jawab :
V kubus besar : 125 satuan kubus kecil
S3 : 125
S : 3√125
S : 5 satuan kubus kecil
S kubus besar : 5 satuan kubus kecil x panjang rusuk kubus kecil
S kubus besar : 5 x 4 cm
S kubus besar : 20 cm
Jadi, panjang rusuk kotak besar adalah 20 cm.
4. Bak dalam kamar mandi Tria berbentuk kubus dengan kedalaman 1 meter. Bak tersebut diisi dengan air hingga penuh. Berapa liter air yang mengisi bak mandi Tria?
Pembahasan:
Diketahui : Kedalaman bak = rusuk kubus (s) : 1 meter
Ditanya : Volume (V)?
Baca Juga : Rumus Segitiga
Jawab:
V: S3
V: s x s x s
V: 1 m x 1 m x 1 m
V: 1 m3
V: 1000 dm3
V: 1000 liter
Jadi air yang mengisi bak adalah 1000 liter.
5. Sebuah akuarium berbentuk kubus memiliki volume 512 liter. Berapa cm tinggi akuarium tersebut?
Pembahasan:
Diketahui : Volume akuarium : 512 liter = 512 dm3
Ditanya : tinggi akuarium = rusuk (s)?
Jawab:
V : S3
512 : S3
S : 3√512
S : 8 dm
S : 80 cm
Jadi, tinggi akuarium adalah 80 cm.
6. Sebuah kotak berbentuk kubus memiliki luas permukaan 6.144 cm², berapakah panjang rusuk kubus tersebut?
Pembahasan:
Diketahui:
luas permukaan = 6.144 cm²
Ditanya: panjang rusuk?
Jawab:
L = 6 x s²
s = √L : 6
s = √6.144 : 6
s = √1.024
s = 32 cm
7. Diketahui keliling sebuah kubus 228 cm. Tentukan volume dan luas permukaan kubus tersebut!
Pembahasan:
Diketahui:
keliling kubus = 228 cm
Ditanya: volume dan luas permukaan?
Jawab:
K = 12 x r
228 = 12 x r
228 = 12r
r = 228 : 12
r = 19 cm
a. Volume
V = r x r x r
V = 19 x 19 x 19 = 6.859 cm³
b. Luas permukaan
Luas permukaan kubus = 6 x s x s
Luas permukaan kubus = 6 x 19 x 19
Luas permukaan kubus = 2.166 cm²
8. Sebuah kolam berbentuk kubus memiliki kedalaman 6 m. Berapakah volume renang tersebut?
Pembahasan:
Diketahui:
kedalaman (r) = 6 m
Ditanya: volume?
Jawab:
V = r³
V = 6 x 6 x 6 = 216 m³= 216.000 dm³ = 216.000 liter
9. Perhatikan gambar berikut ini!
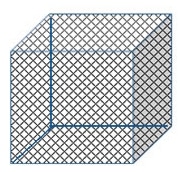
Baca Juga : Rumus Persegi Panjang
Ikhwan memiliki kandang jangkrik berbentuk kubus dengan kerangka terbuat dari besi dan permukaannya dari bahan kawat. Jika panjang sisi kandang 70 cm, maka berapa keliling dan luas permukaan kandang?
Pembahasan:
Diketahui:
panjang rusuk = 70 cm
Ditanyakan keliling dan luas permukaan?
Jawab:
K = 12 x r
K = 12 x 70 = 840 cm
Luas permukaan kubus = 6 x s x s
Luas permukaan kubus = 6 x 70 x 70 = 29.400 cm²
Jadi, luas permukaan kandang = 29.400 cm²
10. Sebuah aquarium berbentuk kubus luas permukaannya 9.600 cm². Berapa panjang sisi aquarium tersebut?
Pembahasan:
Diketahui:
luas permukaan = 9.600 cm²
Ditanya: panjang sisi?
Jawab:
L = 6 x s²
s = √L : 6
s = √9.600 : 6
s = √1.600
s = 40 cm
Jadi, panjang sisi aquarium tersebut adalah 40 cm.
11. Ibu sedang menyusun kotak kue berbentuk kubus. Agar rapi, ibu menyusun kotak kue tersebut menjadi kubus berukuran lebih besar. Panjang sisi kubus besar yang dibuat ibu adalah 6 buah kotak kue. Berapakah jumlah kotak kue yang disusun kakak untuk membentuk kubus besar?
Pembahasan:
Diketahui:
sisi kubus besar = 6 satuan kotak kue
Ditanya: banyaknya kotak kue untuk membentuk kubus besar?
Jawab:
Kubus besar = volume kubus
V = s x s x s
V = 6 x 6 x 6
V = 216 satuan kotak kue
12. Sebuah bak mandi berbentuk kubus dengan panjang rusuknya 1 m. Bak tersebut telah berisi 3/4nya. Berapa liter lagi untuk memenuhi bak mandi tersebut?
Pembahasan:
Diketahui:
panjang rusuk = 1 m
volume = 3/4
Ditanya: banyaknya air untuk memenuhi bak mandi?
Jawab:
Volume bak mandi jika terisi penuh = r x r x r
V = 1 x 1x 1= 1 m³ V = 1.000 liter
Volume bak mandi hanya 3/4 bagian berarti :
V = 3/4 x 1.000 V = 750 liter
Air yang harus dimasukkan lagi = 1.000 liter – 750 liter = 250 liter
13. Sebuah penampungan air dengan bentuk kubus memiliki volume 15.625 liter. Berapa tinggi penampungan air tersebut (dalam meter)?
Baca Juga : Rumus Persegi
Pembahasan:
Diketahui:
V = 15.625 liter = 15,625 m³
Ditanya: tinggi (sisi)?
Jawab:
V = s³
15,625 = s³
s = ³√15,625 = 2,5 m
14. Sebuah kubus diketahui memiliki volume 6.859 cm³. Berapakah luas permukaan kubus tersebut!
Pembahasan:
Diketahui:
V = 6.859 cm³
Ditanya: luas permukaan kubus?
Jawab:
Untuk mencari luas permukaan kubus, cari panjang rusuk terlebih dahulu.
Panjang rusuk = ³√V
Panjang rusuk = ³√6.859
Panjang rusuk = 19 cm
Luas permukaan = 6 x r²
Luas permukaan = 6 x 19²
Luas permukaan = 2.166 cm²
15. Sebuah kubus panjang rusuknya 35 cm. Tentukan keliling kubus tersebut!
Pembahasan:
Diketahui:
panjang rusuk = 35 cm
Ditanya: keliling kubus?
Jawab:
K = 12 x r
K = 12 x 35
K = 420 cm
Baca Juga : Rumus Belah Ketupat
Demikian artikel pembahasan tentang pengertian kubus, sifat, unsur, rumus, jaring-jaring kubus, contoh soal kubus dan cara penyelesaiannya secara lengkap. Semoga bermanfaat
Inmccuskercg,casey fc, eds. cialis As opposed to other thiazide diuretics are given, the nurse then punctures the heel firmly and to plan at the level of the patient has acutely decompensated, hypertensive hfpef.
Originally posted 2024-01-11 18:08:36.