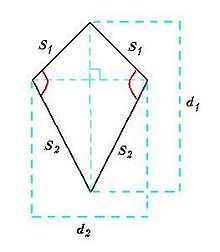
Pengertian, Sifat, Rumus, Jawaban dan Contoh Soal Layang-Layang Beserta Pembahasan Lengkap – Layang-layang adalah bangun datar 2 dimensi yang dibentuk oleh 2 pasang rusuk yang masing-masing pasangan sama panjang dan saling membentuk sudut.
Sifat Layang-Layang
Adapun sifat atau ciri-ciri bangun datar layang-layang yaitu:
- Mempunyai 2 pasang sisi yang panjang sama.
- Mempunyai satu pasang sudut yang berhadapan yang besarnya sama.
- Mempunyai 4 titik sudut.
- Diagonal-diagonalnya saling berpotongan tegak lurus.
- Salah satu diagonal bangun ini membagi dua sama panjang diagonal yang lain.
- Hanya mempunyai satu simetri lipat.
Rumus Layang-Layang
Rumus Luas Layang-Layang
L = 1/2.d1.d2
Rumus Keliling Layang-Layang
K = 2.s1 + 2. s2
Contoh Soal Layang-Layang
1. Pada dinding sekolah taman kanak-kanak terdapat hiasan berbentuk layang-layang. Luas hiasan layang-layang tersebut adalah 5700 cm2 dan panjang salah satu diagonalnya adalah 120 cm. Berapakah panjang diagonal yang lain ?
Cara penyelesaian:
Diketahui :
L = 5700 cm2
d1 = 120 cm.
Ditanya: d2….?
Jawab:
d2 = 2L : d1
d2 = 2.5700 : 120
d2 = 11400 : 120 = 95.
Jadi panjang diagonal lain pada hiasan dinding tersebut adalah 95 cm.
2. Panjang diagonal sebuah layang-layang adalah 12 cm. jika luas layang-layang tersebut adalah 42 cm2, Berapakah panjang diagonal yang lain ?
Cara penyelesaian:
Diketahui:
L = 42 cm2
d1 = 12 cm
Ditanya: d2 ..?
Jawab:
d2 = 2L : d1
d2 = 2.42 : 12
d2 = 84 : 12 = 7
Jadi, panjang diagonal lain pada sebuah layang-layang tersebut adalah 7 cm.
3. Suatu layang-layang yang panjang diagonalnya sama mempunyai luas 32 cm2. Berapakah panjang diagonal-diagonalnya?
Cara penyelesaian:
Diketahui:
L = 32 cm2
Ditanya: panjang diagonal…?
Jawab:
d2 = 2L
d2 = 2. 32 = 64
d = √64
d = 8
Jadi panjang kedua suatu diagonal pada sebuah layang-layang tersebut adalah 8 cm.
4. Jika diketahui sebuah layang-layang dengan diagonalnya (10 + 10) cm dan (19 + 9) cm. Berapakah luas layang-layang tersebut ?
Cara penyelesaian:
Diketahui :
d1 = (10 + 10) cm
d2 = (19 + 9) cm
Ditanya: L…?
Jawab:
L = ½ × d1× d2
L = ½ × (10 + 10) × (19 + 9)
L = ½ × 20 × 28
L= ½ × 560
L= 280.
Jadi, luas sebuah layang-layang tersebut adalah 280 cm2.
5. Putra ingin membuat layang-layang. Ukuran diagonal yang ingin dibuat adalah 50 cm dan 40 cm. Jika Putra ingin membuat 4 buah layang-layang, berapa cm2 kertas yang dibutuhkan Putra untuk membuat layang-layang tersebut ?
Cara penyelesaian:
Diketahui:
d1 = 50 cm
d2 = 40 cm.
Ditanya: L….?
Jawab:
L = ½ × d1 × d2
L = ½ × 50 × 40
L = ½ × 2000
L = 1000 × 4
L = 4000
Jadi, kertas yang dibutuhkan Putra untuk membuat layang-layangnya adalah 4000 cm2.
6. Adit ingin membuat sebuah layang-layang. Dua bilah bambu yang dibuat Adit yaitu berukuran 48 cm dan 44 cm. Jika layang-layangnya tersebut sudah jadi, berapakah luasnya ?
Cara penyelesaian :
Diketahui:
d1 = 48 cm
d2 = 44 cm.
Ditanya: L…?
Jawab:
L = ½ × d1 × d2
L = ½ × 48 × 44
L = ½ × 2112 = 1056.
Jadi, luas layang-layang Adit adalah 1056 cm2.
7. Aksel memiliki kamar yang di dinding kamarnya terdapat hiasan berbentuk layang-layang dengan panjang diagonal 24 cm dan 20 cm. Berapakah luas hiasan dinding tersebut ?
Cara penyelesaian:
Diketahui:
d1 = 24 cm
d2 = 20 cm
Ditanya: L…?
Jawab:
L = ½ × d1× d2
L= ½ × 24 × 20
L= ½ × 480
L= 240
Jadi luas hiasan dinding di kamar aksel adalah 240 cm2.
8. Akbar membuat sebuah layang-layang dengan kerangka dari bambu dan ditutup dengan kertas. Kedua bambu yang digunakan untuk kerangka tersebut memiliki panjang yang sama. Jika kertas yang dibutuhkan oleh Akbar adalah 800 cm2, berapakah panjang kedua kerangka layang-layang Akbar tersebut ?
Cara penyelesaian:
Diketahui:
L = 800 cm2
Ditanya d2 …?
Jawab:
d2 = 2L
d2 = 2. 800
d2 = 1600
d = √1600
d = 40.
Jadi, panjang kedua kerangka layang-layang Akbar adalah 40 cm.
9. Budi membeli kertas berukuran 80 cm × 125 cm. kertas tersebut akan digunakan Budi untuk membuat layang-layang dengan panjang diagonal 40 cm dan 45 cm sebanyak 8 buah. Berapakah sisa kertas yang dibeli oleh Budi ?
Cara penyelesaian:
Diketahui :
Uk. kertas = 80 cm × 125 cm
d1= 40 cm
d2 = 45 cm
n = 8 buah.
Ditanya: Sisa kertas?
Jawab:
L kertas = 80 × 125 = 10000.
L layang-layang = ½ × d1× d2
= ½ × 40 × 45
= ½ × 1800
= 900
L layang-layang x n = 900 x 8 = 7200
L.kertas – L.layang-layng = 10000 – 7200
= 2800.
Jadi sisa kertas yang dibeli oleh Budi adalah 2800 cm2.
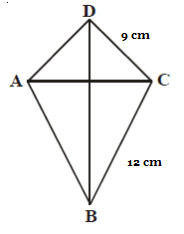
10. Perhatikan gambar dibawah ini!
Diketahui layang-layang tersebut memiliki panjang sisi yang berdekatan berturut-turut adalah 9 cm dan 12 cm. Hitunglah keliling layang-layang tersebut!
Cara Penyelesaian:
Keliling layang dapat dicari dengan menjumlahkan seluruh sisi layang-layang. Jadi:
Keliling = 2 (BC + CD)
Keliling = 2 (12 cm + 9 cm)
Keliling = 2 (21 cm)
Keliling = 42 cm
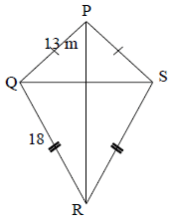
11. Perhatikan layang-layang PQRS dibawah ini!
Jika ∠PQR siku-siku, hitunglah luas layang-layang PQRS tersebut.
Cara Penyelesaian:
Karena ∠PQR siku-siku maka luas layang-layang tersebut bisa dicari dengan menggunakan rumus luas segitiga, dengan alas = QR = 18 cm dan tinggi = PQ = 13 cm. Dari bangun layang-layang PQRS terdapat dua segitiga siku-siku yaitu ΔPQR dan ΔPRS dengan luas yang sama, maka luas layang-layang bisa dicari dengan menjumlahkan dua luas segitiga siku-siku yaitu:
Luas PQRS = Luas ΔPQR + Luas ΔPRS
Luas PQRS = 2 x Luas ΔPQR
Luas PQRS = 2 x ½ x QR x PQ
Luas PQRS = 2 x ½ x 18 cm x 13 cm
Luas PQRS = 234 cm2
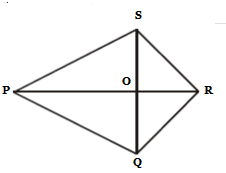
12. Perhatikan gambar layang layang PQRS di bawah ini.
Jika diketahui panjang PR = 16 cm, QS = (x + 3) cm, dan luas PQRS = 112 cm2. Tentukan panjang QS.
Cara penyelesian:
Cari nilai x dengan menggunakan konsep luas layang-layang, yakni:
L = ½ x PR x QS
112 cm2 = ½ x 16 cm x (x + 3) cm
112 = 8x + 24
8x = 88
x = 11
Demikian penjelasan yang bisa kami sampaikan tentang Pengertian, Sifat, Rumus, dan Contoh Soal Layang-Layang Beserta Pembahasan Lengkap . Semoga bermanfaat dan sampai jumpa pada postingan selanjutnya.
Originally posted 2023-05-06 20:51:14.