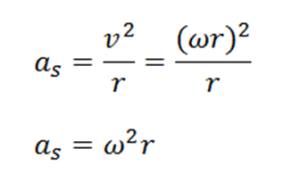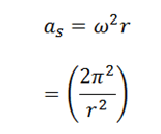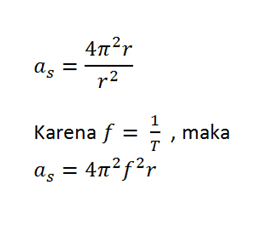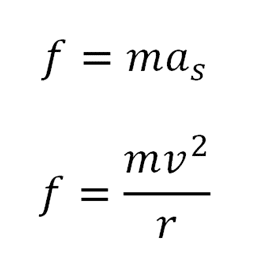Pengertian, Rumus Dan Contoh Percepatan dan Gaya Sentripetal Terlengkap

Pada Gambar 3.3 berikut ini ditunjukkan bagaimana sebuah benda bisa bergerak dengan lintasan melingkar. Pada gambar (a), sebuah mobil mula-mula bergerak ke timur dengan kecepatan v₁ kemudian berbelok ke selatan dengan kecepatan v₂. Bila kelajuan mobil sepanjang gerakannya adalah konstan,artinya v₁ = v₂ = v₂ , maka kecepatan mobil berubah semata-mata disebabkan perubahan arah geraknya. Perubahan kecepatan dapat kita tuliskan sebagai ∆v = v₂ – V₁. Dari adanya perubahan kecepatan ini, kita bisa menyimpulkan bahwa dalam gerakan mobil ini terjadi percepatan, karena percepatan merupakan perubahan kecepatan. Dengan menggunakan diagram vektor, kita dapat menggambar dan mencari arah percepatan tersebut.

Pada Gambar (b) dan (c) tampak gerakan mobil yang sama seperti pada Gambar (a) jika dibagi menjadi lintasan-lintasan melingkar yang lebih pendek, yang dimaksudkan untuk menjelaskan terjadinya perubahan kecepatan dari V₁ menjadi v₂. Dari gambar tampak bahwa percepatan mengarah ke suatu tempat yang sama, yaitu pusat lingkaran. Dengan demikian, kita simpulkan bahwa arah percepatan dalam gerak melingkar beraturan adalah ke pusat lingkaran. Percepatan yang selalu mengarah ke pusat lingkaran ini disebut percepatan sentripetal. Berapakah besamya percepatan sentripetal ini?

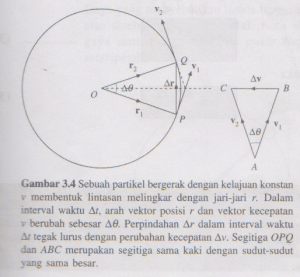
Untuk menghitung besar percepatan sentripetal ini, kita akan menggunakan bantuan diagram vektor sebagaimana ditunjukkan pada Gambar 3.4. Kita misalkan sebuah benda bergerak dari titik P ke titik Q dalam suatu lintasan melingkar dengan jari-jari r. Selama selang waktu ∆t, vektor posisi r telah berputar sejauh ∆ϴ, dan perpindahan benda dinyatakan dengan ∆r = r2 – r₂ Karena v selalu tegak lurus vektor perpindahan r, maka v dan r berubah arah dengan sudut yang sama besar dalam selang waktu yang sama. Dari gambar bisa kita simpulkan bahwa

Dari persamaan yang menyatakan v=ωr, maka percepatan a_s dapat kita tuliskan dalam bentuk

Persamaan (3,7) juga bias kita tuliskan dalam r dan T atau dalam r dan f sebagai berikut

untuk lebih jelasnya perhatikan contoh dibawah ini:

Sesuai dengan hukum II Newton, maka bisa disimpulkan bahwa percepatan sentripetal a_sditimbulkan oleh adanya sebuah gaya yang besamya dapat dituliskan sebagai

Gaya yang menyebabkan benda bergerak dengan percepatan sentripetal as di atas disebut gaya sentripetal. Kata sentripetal menunjukkan bahwa arah gaya sentripetal adalah ke pusat lingkaran, searah dengan percepatan sentripetal.

Dengan perkataan lain gaya sentripetal adalah resultan dan seniua gaya dan komponen gaya pada arah radial dengan mengambil arah menuja pusat lingkaran adalah positifdan arah menjaufti pusat adalah negatif.

Kadang-kadang, pembahasan gerak melingkar beraturan juga memper- kenalkan apa yang dinamakan gaya sentrifugal di samping gay a sentripetal. Jika tidak benar-benar memahami perbedaan keduanya, kita bisa terjebak dengan mengatakan bahwa gaya sentripetal dan gaya sentrifugal menyebabkan benda berada dalam keadaan seimbang. Gaya sentrifugal adalah gaya yang arahnya keluar dari pusat lingkaran. Sebagai contoh, ketika kita memutar sebuah batu yang kita ikatkan pada seutas tali, kita akan merasakan bahwa tangan kita tertarik oleh batu ke arah luar.

Banyak yang beranggapan bahwa gaya sentrifugal dan sentripetal yang sama besar, dan berlawanan arah inilah yang menyebabkan batu bisa melakukan gerak melingkar beraturan. Anggapan ini salah!

Kedua gaya tersebut bekerja pada benda yang berbeda; gaya sentripetal bekeija pada batu, sedangkan gaya sentrifugal bekerja pada tangan kita.

Demikian penjelasan yang bisa kami sampaikan tentang Pengertian, Rumus Dan Contoh Percepatan dan Gaya Sentripetal Terlengkap. Semoga postingan ini bermanfaat bagi pembaca dan bisa dijadikan sumber literatur untuk mengerjakan tugas. Sampai jumpa pada postingan selanjutnya.

Baca postingan selanjutnya: