Materi Lengkap Trigonometri Dengan Fungsi , Rumus Dan Pembahasan Contoh Soal
Dalam merancang kerangka sebuah jembatan perhitungan yang dilakukan tidaklah mudah. Beban, tegangan, serta gaya yang bekerja pada jembatan menjadi pertimbangan utama para perancang untuk mengonstruksikan model rancangannya. Proses ini didasarkan atas pengetahuan dari bangsa Romawi bahwa busur dapat menjangkau jarakyang lebih jauh dan menahan berat yang lebih berat daripada lintel (bentuk balok yang lurus horizontal). Atas dasar ini semakin banyak pula jembatan berbentuk busur yang dibangun. Penggunaan bentuk busur ini melibatkan kelengkungan yang perlu diperhitungkan kemiringan sudutnyayang diberikan dalam persamaan trigonometri. Lebih lanjut mengenai persamaan trigonometri akan Anda pelajari pada uraian berikut.
A. Perbandingan Trigonometri
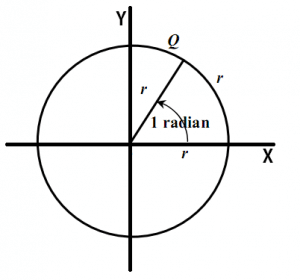
Perhatikan lingkaran dengan pusat O (0, 0) dan jari-jari (r), sedangkan titik A (x, y) pada lingkaran dan sudut dibentuk oleh OA terhadap sumbu X. Pada berlaku r2 = x2 + y2 sehingga diperoleh perbandingan trigonometri sebagai berikut.

1. Rumus Jumlah dan Selisih dua Sudut
a. Rumus untuk Cosinus jumlah selisih dua sudut
cos (A + B) = cos A cos B – sin A sin B cos
(A – B) = cos A cos B + sin A sin B
b. Rumus untuk Sinus Jumlah dan Selisih Dua Sudut
sin (A + B) = sin A cos B + cos A sin B sin
(A – B) = sin A cos B – cos A sin B
c. Rumus untuk Tangen Jumlah dan Selisih Dua Sudut
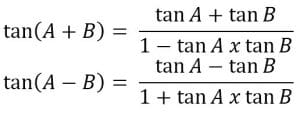
Jika tan 5°= p tentukan tan 50° Jawab : a. Dengan menggunakan rumus sin (A+ B) untuk A = B, maka diperoleh: sin 2A = sin (A + B) b. Dengan menggunakan rumus cos (A + B) untuk A = B, maka diperoleh: cos 2A = cos (A + A) Atau Cos 2A = cos2A-sin2A Atau Cos 2A = cos2A-sin2A Dari persamaan (1) (2) (3) didapatkan rumus sebagai berikut. Cos 2A = cos2 A – sin2 A c. Dengan menggunakan rumus tan (A+B) untuk A=B, diperoleh a. Rumus Perkalian Sinus dan Kosinus Tentukan nilai dari: 2 cos 75° cos 15° Jawab: 2 cos 75° cos 15° = cos (75 +15)° + cos (75 – 15)° b.Rumus Penjumlahan dan Pengurangan Sinus dan Kosinus Tentukan nilai dari sin 105° + sin 15° jawab: sin 105° + sin 15° = 2 sin ½ (105+15)°cos ½ (105-15)° Rumus rumus dasar identitas trigonometri sebagai berikut. Untuk membuktikan suatu persamaan mempakan identitas atau bukan maka persamaan itu diubah dengan salah satu dari cara-cara berikut. Buktikan bahwa sin4 α – sin2 α = cos4 α – cos2 α Jawab. sin4 α – sin2 α = (sin2 α)2 – sin2 α Demikian penjelasan yang bisa kami sampaikan tentang Materi Lengkap Trigonometri Dengan Fungsi , Rumus Dan Pembahasan Contoh Soal. Semoga postingan ini bermanfaat bagi pembaca dan bisa dijadikan sumber literatur untuk mengerjakan tugas. Sampai jumpa pada postingan selanjutnya.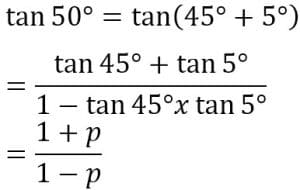
2. Rumus Trigonometri untuk sudut rangkap
= sin A cos A + cos A sin A
= 2 sin A cos A
Jadi,sin2A =2 sin A cos A
= cos A cos A-sin A sin
A = cos2A-sin2A ……………(1)
= cos2 A- (1 – cos2 A)
= cos2 A – 1 + cos2 A
= 2 cos2 A – 1 ……….(2)
= (1 -sin2A)-sin2A
= 1 – 2 sin2A ………. (3)
= 2 cos2 A-1
= 1 – 2 sin2 A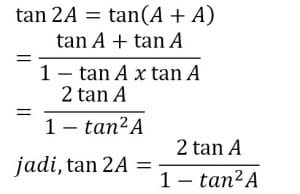
B. Perkalian, Penjumlahan, dan Pengurangan Sinus dan Kosinus
= cos 90° + cos 60°
= 0 + ½
= ½
![]()
![]()
= 2 sin ½ (102)° cos ½ (90)°
= sin 60° cos 45°![]()
C. Identitas Trigonometri
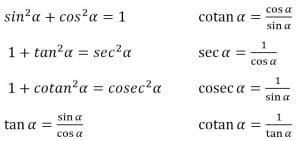
= (1 cos2 α) 2 – (1 cos2 α)
= 1 – 2 cos2 α + cos4 α – 1 + cos2 α
= cos4 α – cos2 α