Hukum Termodinamika 1 dan 2,Penjelasan, Rumus dan Contoh Pembahasan Soal Lengkap!

Sebelum membahas artikel ini ada baiknya para pembaca sudah memahami apa pengertian dari termodinamika yang sudah kita bahas pada artikel sebelumnya yaitu Termodinamika – Rumus Usaha Dan Proses Proses Dalam Termodinamika Lengkap Pembahasan Soal . Sebagai ulasan Termodinamika merupakan salah satu ilmu fisika yang membahas tentang suhu, kalor, dan besaran lain yang berkaitan. Sebagai contoh yaitu Air Conditioner (AC), AC adalah sistem atau mesin yang dirancang untuk menstabilkan suhu udara dan kelembapan suatu area. Alat ini dapat digunakan untuk mendinginkan suhu ruangan sesuai keinginan. Cara kerja AC berkaitan pada materi termodinamika.

Setelah kita paham apa yang dimaksud dengan termodinamika, kali ini kita bahas materi selanjutnya yang masih berhubungan erat dengan termodinamika, yaitu Hukum I dan II Termodinamikan. Untuk lebih jelasnya mari kita simak uraian dibawah ini.

Contents hide

1 Hukum I Termodinamika dan Kapasitas Kalor Gas

2 Hukum I Termodinamika

2.1 Q = ∆U+W

3 Kapasitas Kalor Gas

3.1 W=p∆V=p(V2-V1)

3.2 Cp* = cv* + R

3.3 Contoh soal!

3.4 Siklus Termodinamika dan Hukum II Termodinamika

4 1. Pengertian Siklus

5 2. Siklus Carnot

6 3. Mesin Kalor Carnot

6.1 W = Qt – Qy

6.2 W= Qt — Qr

7 4. Entropi dan Hukum II Termodinamika

7.1 ∆S = S2 – S1 = Q/T

7.2 Hukum II Termodinamika

7.3 Contoh soal!

7.4 Baca postingan selanjutnya:

Hukum I Termodinamika dan Kapasitas Kalor Gas

Hukum I Termodinamika

Hukum I Termodinamika menyatakan bahwa:

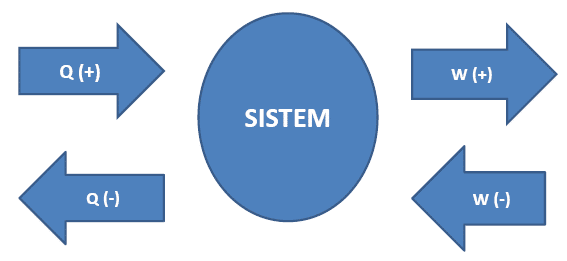
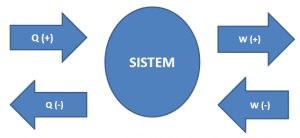
“Sejumlah kalor Q yang diterima dan usaha W yang dilakukan terhadap suatu gas dapat digunakan untuk mengubah energi dalam”.

Secara matematis hukum I termodinamika dapat dirumuskan sebagai berikut:

Q = ∆U+W

Dengan ketentuan, jika:
Q(+) → sistem menerima kalor
OR → sistem melepas kalor
W(+) → sistem melakukan usaha
W(-) → sistem dikenai usaha
∆U(+) → terjadi penambahan energi dalam
∆U(-) → terjadi penurunan energi dalam

Kapasitas Kalor Gas

a. Konsep Kapasitas Kalor Gas

Kapasitas kalor merupakan jumlah kalor yang diperlukan untuk menaikkan temperatur suatu zat sebesar satu kelvin atau satu derajat celcius. Secara matematis, dapat dituliskan:

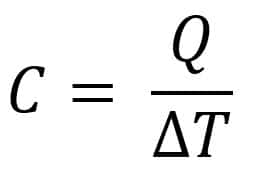dengan C = kapasitas kalor (J/K atau J/°C)

Kalor jenis merupakan kapasitas kalor tiap satuan massa. Secara matematis dapat ditulis:

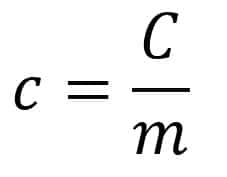dengan c = kalor jenis (J/kg atau J/kgºC)

Kalor jenis molar merupakan kapasitas kalor tiap mol, dinyatakan:

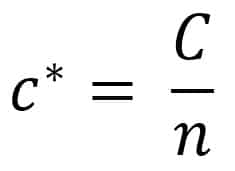dengan c* = kalor jenis molar (J/mol K atau J/mol°C)

b. Macam-Macam Kapasitas Kalor

Kapasitas kalor gas pada tekanan tetap C_p adalah kalor yang diperlukan untuk menaikkan suhu zat sebesar satu kelvin dan tekanan tetap.
Persamaannya adalah:

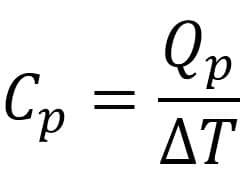
Kapasitas kalor gas pada volume tetap C_v adalah kalor yang diperlukan untuk menaikkan suhu zat sebesar satu kelvin pada volume tetap.
Persamaannya adalah:

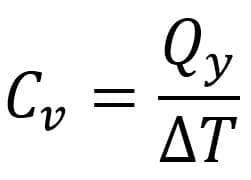
Hubungan C_p dan C_v adalah:

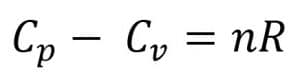
Dari berbagai persamaan, usaha dapatdinyatakan:

W=p∆V=p(V₂-V₁)

W=nR∆T=nR(T₂-T₁)

W=Q_p-Q_v = (C_p-C_v)∆T

Untuk kalor jenis molar, persamaan matematisnya:

**C_p* = c_v* + R**

Gas monoatomic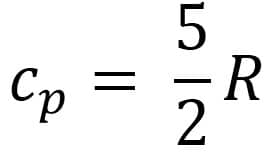

Gas diatomic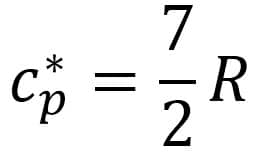

Tetapan Laplace (Ƴ) merupakan perbandingan C_p terhadap C_v. Untuk gas monoatomik Ƴ = 1,67, sedangkan gas diatomik Ƴ = 1,4.

Contoh soal!

1. Suatu gas dalam ruang tertutup melepaskan kalor ke lingkungan sebesar 1.000 kalori dan melakukan usaha 2.000 joule. Berapakah perubahan energy dalam gas? (1 kalori = 4,2 J)

Penyelesaian:

Diketahui :
Q = -1.000 kalori = -4.200 J
W = +2.000 J

Ditanyakan : ∆U

Jawab:

∆U = Q –W
= -4.200 J – (+2.000 J)
= -6.200 J

2. Gas hydrogen dipanaskan dari suhu 300 K sampai 312 K dalam bejana yang bebas hingga memuai. Kalor yang dibutuhkan dalam proses itu 24kJ. Tentukan kapasitas kalor hydrogen!

Penyelesaian:

Diketahui :
∆T = 312 K – 300 K = 12 K
Q_p = 24 kJ = 24.000 J

Ditanyakan : C_p ?

Jawab :

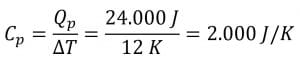
Siklus Termodinamika dan Hukum II Termodinamika

1. Pengertian Siklus

Siklus adalah serangkaian proses yang dimulai dari suatu keadaan awal dan berakhir pada keadaan yang sama dengan keadaan awalnya. Agar dapat melakukan usaha terus-menerus, suatu sistem harus bekerja dalam satu tsiklus. Ada 2 macam siklus, yaitu siklus reversibel (siklus yang dapat balik) dan irreversibel (siklus yang tidak dapat balik).

2. Siklus Carnot

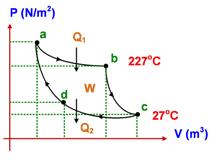
Perhatikan gambar diatas. Gambar diatas merupakan gambar siklus mesin pemanas carnot. terdapat empat proses dalam siklus Carnot, yaitu:

pemuaian secara isotermik. (a-b)
pemuaian secara adiabatik. (b-c)
pemampatan secara isotermik. (c-d)
pemampatan secara adiabatik. (d-a)

3. Mesin Kalor Carnot

Proses-proses dalam mesin kalor Carnot, perhatikan gambar siklus carnot diatas. Siklus dapat dijelaskan sebagai berikut:

Siklus a-b
Gas menyerap kalor Qt pada temperatur Tv Suhu sistem sama dengan suhu reservoir panas sehingga disebut proses isotermik. Gas memuai dan melakukan usaha pada pengisap. Oleh karena energi dalam tetap maka usaha yang dilakukan pada sistem sama dengan kalor yang diserap.
Siklus b-c
Beban pengisap dikurangi sehingga gas memuai menurut proses adiabatik. Terjadi pengurangan energi dalam dan suhu sistem menurun sampai sama dengan suhu pada reservoir dingin Tr
Siklus c-d
Gas mengalami penyusutan secara isotermik dengan membuang kalor Qrpada reservoir dingin pada temperatur 7) sehingga usahanya negatif (usaha dilakukan pada sistem).
Siklus d-1
Beban pengisap ditambah sehingga gas menyusut menurut proses adiabatik. Terjadi penambahan energi dalam dan suhu naik sampai sama dengan suhu pada reservoir panasT,. Energi dalam gas kembali seperti pada awal siklus.

Usaha pada mesin pemanas Carnot:

W = Q_t – Q_y

Karakteristik mesin kalor carnot dinyatakan dengan efisiensi mesin (η) yaitu perbandingan antara usaha yang dilakukan dengan kalor yang diserap. Secara matematis ditulis sebagai berikut.

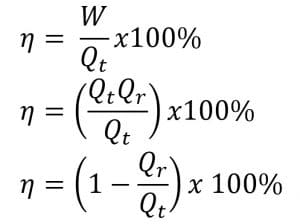
Efisiensi suatu mesin kalor jenis apa pun selalu lebih kecil dari efisiensi mesin ideal atau mesin Carnot.

Berdasarkan hukum I Termodinamika berlaku:

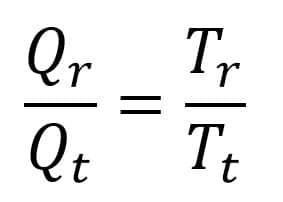
Keterangan:
η = efisiensi mesin
T_r = temperatur pada reservoir rendah
T_t = temperatur pada reservoir tinggi
Q_r = kalor yang dibuang pada reservoir rendah
Q_t = kalor yang diserap pada reservoir tinggi

Mesin Pendingin Carnot

Contoh dari mesin pendingin Carnot antara lain mesin pendingin ruangan dan lemari es. Siklus mesin pendingin Carnot merupakan kebalikan siklus mesin kalor Carnot karena siklusnya reversibel (dapat balik).

Usaha pada mesin pendingin Carnot dapat dituliskan:

W= Q_t — Q_r

Karakteristik pada mesin pendingin dinyatakan dengan koefisien performansi atau koefisien kinerja yang simbolnya K_d. Koefisien kinerja didefinisikan sebagai perbandingan antara kalor yang dipindahkan dengan usaha yang dilakukan sistem.

Mesin Pemanas Carnot

Dari Gambar 4.9 dapat dijelaskan bahwa kalor yang diambil dipindahkan ke dalam ruangan.
Karakteristik mesin pemanas dinyatakan dengan koefisien kerja yang simbolnya K_p . Secara matematis dapat dituliskan:

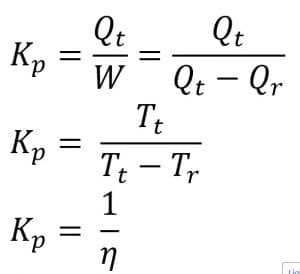
4. Entropi dan Hukum II Termodinamika

Entropi

Entropi dapat diartikan sebagai ukuran ketidakteraturan. Dalam sistem tertutup peningkatan entropi diikuti oleh penurunan jumlah energi yang tersedia. Semakin tinggi entropi, semakin tinggi ketakteraturannya.

Entropi pada Proses Temperatur Konstan
Jika suatu sistem pada suhu mutlak T mengalami proses reversibel dengan menyerap sejumlah kalor Q maka kenaikan entropi ∆S dapat dituliskan:
∆S = S₂ – S₁ = Q/T

Keterangan:
∆S= perubahan entropi (J/K)
S₁ = entropi mula-mula (J/K)
S₂ = entropi akhir (J/K)

Entropi pada Proses Temperatur Berubah
Pada proses yang mengalami perubahan temperatur, entropi dituliskan sebagai berikut.

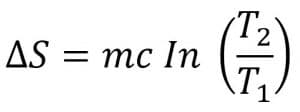
Keterangan:
∆S = perubahan entropi (J/K)
S₁= entropi mula-mula (J/K)
S₂ = entropi akhir (J/K)
c = kalor jenis (J/kg K)
m = massa (kg)
T₁= suhu mula-mula (K)
T₂ = suhu akhir (K)

Hukum II Termodinamika

Bunyi hukum II Termodinamika:

” Kalor mengalir secara alami dari benda yang panas ke benda yang dingin; kalor tidak akan mengalir secara spontan dari benda dingin ke benda panas tan pa dilakukan usaha”.

Penjelasan hukum II Termodinamika adalah sebagai berikut.

Tidak mungkin membuat mesin yang bekerja dalam satu siklus, menerima kalor dari satu reservoir dan mengubah kalor seluruhnya menjadi usaha.
Tidak mungkin membuat mesin yang bekerja dalam satu siklus dengan mengambil kalor dari reservoir yang mempunyai suhu rendah dan memberikannya ke reservoir suhu tinggi tanpa usaha dari luar.
Mesin yang bekerja di antara reservoir suhu T_t dan reservoir suhu T_t(T_t > T_r), memiliki efisiensi maksimum.

Contoh soal!

1. Suatu mesin memiliki suhu reservoir tinggi 400°C dan suhu reservoir rendah 70°C. Hitunglah efisiensi mesin tersebut!

Penyelesaian:

Diketahui :
Tt = 400°C = 673 k
Tr = 70°C = 343 K

Ditanyakan : η

Jawab:

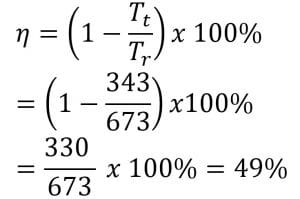
Jadi, efisiensi mesin sebesar 49%

2. Suatu system menyerap kalor sebesar 60 kJ pada suhu 27°C. Berapakah peubahan entropi system ini?

Penyelesaian:

Diketahui:
Q = 60 kJ = 60. 000J
T = 27°C = 300 K

Ditanyakan:

Jawab:

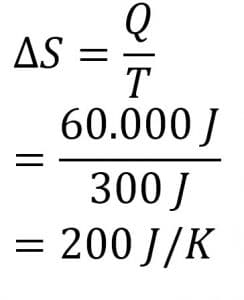
Jadi, besar perubahan entropi adalah 200J/K

Demikian penjelasan yang bisa kami sampaikan tentang Hukum Termodinamika I dan II,Penjelasan, Rumus dan Contoh Pembahasan Soal. Semoga postingan ini bermanfaat bagi pembaca dan bisa dijadikan sumber literatur untuk mengerjakan tugas. Sampai jumpa pada postingan selanjutnya.