Bunyi Hukum Kepler 1 2 3 – Apa yang dimaksud hukum Kepler? Apa yang dimaksud Hukum Kepler 1 2 3? Bagaimana bunyi hukum Kepler? Bagaimana hukum Newton menjelaskan tentang hukum Kepler? Apa Perbedaan Hukum Kepler 1 dan Hukum Kepler 2? Jelaskan bagaimanakah hubungan antara hukum Kepler 3 dengan hukum Newton? Bagaimana kecepatan planet ketika jauh dan dekat dari Matahari?
Baca Juga : Hukum Newton 1 2 3
Agar lebih memahaminya, kali ini kita akan membahas tentang pengertian hukum kepler, bunyi hukum kepler 1, 2, 3, fungsi, rumus dan contoh soal hukum kepler secara lengkap.
Pengertian dan Sejarah Hukum Kepler
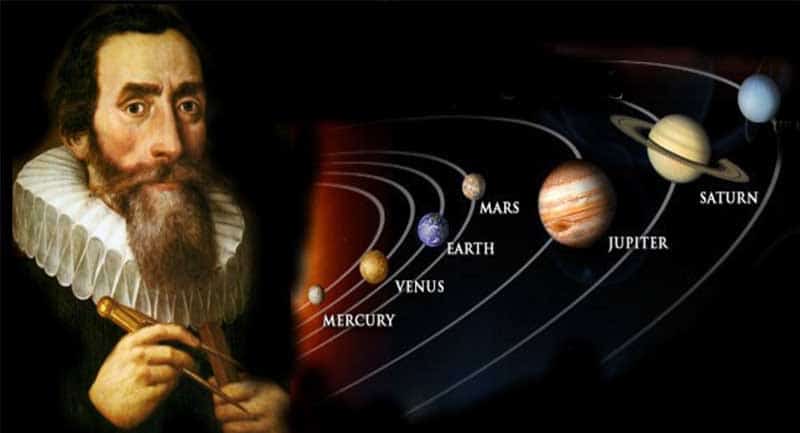
Hukum Kepler atau Hukum Gerakan Planet Kepler ditemukan oleh seorang matematikawan yang juga seorang astronom Jerman bernama Johannes Kepler (1571-1630). Penemuan tersebut didasari oleh data yang diamati Tycho Brahe (1546-1601), yaitu seorang astronom Denmark.
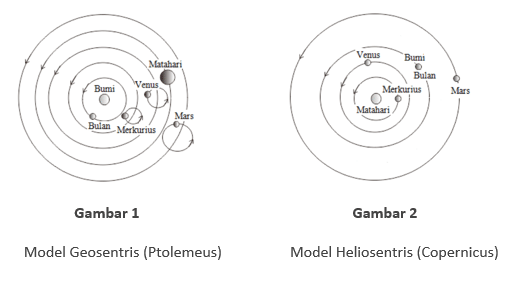
Sebelum ditemukan hukum kepler, manusia menganut paham geosentris, yaitu paham yang membenarkan bahwa bumi merupakan pusat alam semesta. Anggapan tersebut didasari pada pengalaman indrawi manusia yang terbatas, yang setiap hari mengamati matahari, bulan dan bintang bergerak, sedangkan bumi dirasakan diam. Anggapan tersebut dikembangkan oleh astronom Yunani Claudius Ptolemeus (100-170 M) dan bertahan hingga 1400 tahun. Menurut Claudius Ptolemeus, bumi berada di pusat tata surya. Matahari dan planet-planet mengelilingi bumi dalam lintasan melingkar.
Kemudian pada tahun 1543, seorang astronom Polandia bernama Nicolaus Copernicus (1473-1543) mencetuskan model heliosentris. Heliosentris berarti bumi beserta planet lainnya mengelilingi matahari dalam lintasan yang melingkar. Tentu saja pendapat tersebut lebih baik dibanding pendapat sebelumnya. Akan tetapi, ada yang masih kurang dari pendapat Copernicus yaitu diam masih menggunakan lingkaran sebagai bentuk lintasan gerak planet.
Pada tahun 1596, Kepler menerbitkan buku pertamanya di bidang astronomi “The Mysteri of the Universe”. Dalam buku tersebut, ia memaparkan kekurangan dari kedua model diatas yaitu tiada keselarasan antara lintasan orbit planet dengan data pengamatan Tycho Brahe. Untuk itu, Kepler meninggalkan model Copernicus dan juga Ptolemeus kemudian mencari model baru. Pada tahun 1609, ditemukan bentuk orbit yang cocok dengan data pengamatan Brahe, yaitu bentuk elips. Selanjutnya, penemuannya dipublikasikan dalam bukunya “Astronomia Nova” yang juga disertai hukum keduanya. Sedangkan hukum ketiga Kepler tertulis dalam “Harmonices Mundi” yang dipublikasikan sepuluh tahun kemudian.
Bunyi Hukum Kepler 1, 2, 3
Hukum 1 Kepler
Hukum I Kepler menjelaskan bagaimana bentuk lintasan orbit planet-planet. Hukum I Kepler dikenal sebagai hukum lintasan elips. Bunyi Hukum I Kepler:
“Setiap planet bergerak dengan lintasan elips, Matahari berada di salah satu fokusnya.”
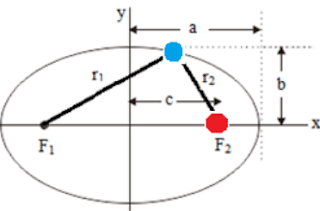
Model diatas memperlihatkan bentuk elips dari lintasan orbit planet yang mengelilingi matahari. Dimana matahari berada di salah satu titik fokusnya (ditandai dengan F1 dan F2). Sedangkan planet berada pada jarak r2 dari F2 atau r1 dari F1. Jika posisi planet berubah maka jarak r1 dan r2 ikut berubah. Jarak a disebut sumbu semi mayor dan 2a disebut mayor. Jarak b disebut sumbu semi minor dan 2b disebut minor. Jarak c dari titik pusat merupakan titik fokus, dimana c2 = a2+b2.
Baca Juga : Hukum Ohm
Bentuk eklips orbit ditentukan oleh eksentrisitas (e) elips tersebut. Semakin kecil eksentrisitasnya, maka bentuk elipsnya akan semakin mendekati bentuk lingkaran. Dan sebaliknya, jika eksentrisitasnya semakin besar, bentuk elips akan memanjang dan tipis. Jarak merupakan perbandingan dari jarak c dengan jarak a (e = c/a). Nilai eksentrisitas elips lebih besar dari 0 dan lebih kecil dari 1.
Saat planet berada pada jarak terjauh dari matahari, maka planet berada pada titik aphelion (terletak di ujung kiri eklips (sebelah kiri F1) pada gambar diatas). Jarak dari aphelion ke matahari bisa dihitung dengan menjumlahkan jarak a dengan c. Jika planet berada pada ujung kanan elips (sebelah kanan F2) maka planet sedang berada pada titik perihelion. Pada saat itu, planet berada pada jarak terdekat dengan matahari. Jarak perihelion dengan matahari merupakan selisih antara jarak a dengan c.
Hukum I Kepler menyatakan bentuk orbit planet, namun tidak bisa memperkirakan kedudukan planet pada suatu saat. Karena hal tersebut, Kepler berusaha memecahkan persoalan tersebut, kemudian berhasil menemukan hukum II Kepler.
Hukum 2 Kepler
Hukum Kepler II menyatakan tentang kecepatan orbit suatu planet. Bunyi hukum II yaitu :
“Setiap planet bergerak sedemikian sehingga suatu garis khayal yang ditarik dari matahari ke planet tersebut mencakup daerah dengan luas yang sama dalam waktu yang sama.”
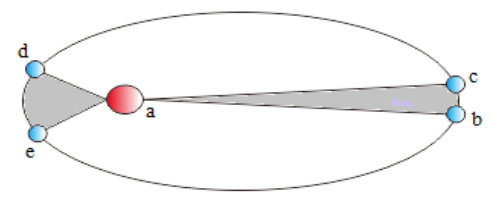
Pada gambar diatas diperlihatkan dua contoh luasan yaitu luasan aphelion (abc) dan luasan perihelion (ade) untuk menjelaskan hukum II Kepler. Kedua luasan tersebut memiliki luas yang sama. Pada selang waktu yang sama, garis khayal yang menghubungkan planet dan matahari menyapu luasan yang memiliki besar yang sama. Oleh karena itu, saat planet bergerak dari b ke c (titik aphelion), kecepatan orbit planet lebih kecil atau lambat. Sedangkan saat planet bergerak dari d ke e (titik perihelion) kecepatan orbit planet lebih besar atau cepat. Maka dapat disimpulkan, keceptan orbit maksimum planet yaitu saat planet berada di titik perihelion dan kecepatan minimumnya saat berada di titik aphelion.
Hukum 3 Kepler
Hukum Kepler III menjelaskan mengenai periode revolusi setiap planet yang melilingi matahari. Bunyi Hukum Kepler III yaitu:
“Kuadrat perioda suatu planet sebanding dengan pangkat tiga jarak rata-ratanya dari Matahari.”
Secara sistematis, persamaan hukum 3 kepler ditulis:
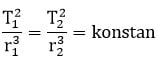
Keterangan :
T1 = Periode planet pertama
T2 = Periode planet kedua
r1 = jarak planet pertama dengan matahari
r2 = jarak planet kedua dengan matahari
Persamaan tersebut bisa diturunkan dengan menggabungkan 2 persamaan hukum Newton yaitu hukum gravitasi Newton dan hukum II Newton untuk gerak melingkar beraturan. Penurunan rumusnya yaitu:
Persamaan Hukum Newton II
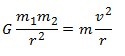
Keterangan :
m = massa planet yang mengelilingi matahri
a = percepatan sentripetal planet
v = kecepatan rata-rata planet
r = jarak rata-rata planet dari matahari
Persamaan Hukum Gravitasi Newton
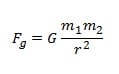
Keterangan:
Fg = Gaya gravitasi matahari
m1 = massa matahari
m2 = massa planet
r = jarak rata-rata planet dan matahari
Kedua rumus tersebut kemudian digabungkan menjadi:
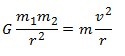
m2 pada ruas kiri dan m pada ruas kanan merupakan massa planet sehingga dapat dihilangkan.
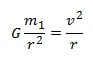
Panjang lintasan yang dilalu planet merupakan keliling lintasan orbit planet. Keliling orbit planet dapat dirumuskan dengan 2 x phi x r, dimana r adalah jarak rata-rata planet dari matahari. Diketahui bahwa kecepatan rata-rata planet merupakan perbandingan antara keliling orbit dan periode panet, sehingga dapat ditulis:
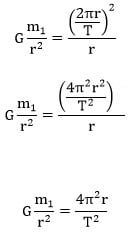
Baca Juga : Hukum Archimedes
Konstanta k = T2/r3 yang diperoleh oleh Kepler ditemukan dengan cara perhitungan menggunakan data astronomi Tycho Brahe. Hasilnya sama dengan yang diperoleh menggunakan rumus kedua Hukum Newton diatas.
Fungsi Hukum Kepler
Di kehidupan modern, hukum kepler digunakan untuk memperkirakan lintasan planet atau benda luar angkasa lainnya yang mengorbit Matahari seperti asteroid atau planet luar yang belum ditemukan semasa Kepler hidup. Selain itu, hukum kepler juga digunakan pada pengorbitan lainnya selain matahari; seperti bulan yang mengorbit bumi, bahkan saat ini dengan menggunakan dasar hukum Kepler ditemukan benda baru yang mengorbit bumi selain bulan. Benda tersebut merupakan sebuah asteroid yang berukuran 490 kaki (150 meter) yang dijuluki dengan Asteroid 2014 OL339. Asteroid berada cukup dekat dengan bumi sehingga terlihat seperti satelitnya. Asteroid tersebut memiliki orbit elips. Asteroid tersebut membutuhkan waktu 364,92 hari untuk mengelilingi Matahari. Hampir sama dengan bumi yang memiliki periode 365,25 hari.
Contoh Soal Hukum Kepler
Berikut ini beberapa contoh soal hukum kepler dan cara penyelesaiannya:
1. Waktu yang diperlukan bumi untuk mengelilingi matahari yaitu 1 tahun dan jarak rata-rata antara bumi dengan pusat tata surya nya yaitu 1,5 x 1011 m. Jika diketahui ternyata periode orbit planet venus adalah 0,615 tahun, berapa jarak antara matahari dengan venus?
Pembahasan:
Diketahui:
Periode bumi = Tb = 1 tahun
Jarak matahari ke bumi Rm-b = 1,5 x 1011 m
Periode venus = Tv = 0,615 tahun
Ditanya:Rm-v…?
Jawab:
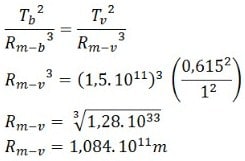
Dengan menggunakan hukum kepler III, jawabannya yaitu jarak antara matahari dan planet venus adalah 1,084 x 1011 m (lebih dekat daripada bumi).
2. Untuk mengelilingi matahari, bumi membutuhkan waktu tempuh selama 1 tahun. Jarak tempuh antara matahari dan bumi adalah sebesar 1, 6 x 1011 Jika periode orbit dari planet Mars adalah 0,5 tahun, berapakah jarak antara planet Mars dengan matahari?
Pembahasan:
Diketahui:
Waktu tempuh atau periode bumi (Tb) = 1 tahun
r1 = 1,6 x 1011 m
waktu tempuh Mars (Tm) = 0,5 tahun
Ditanyakan: r2?
Jawab:
(Tb)2/(r1)3 = (Tm)2/(r2)3
(1)2/(1,6 x 1,011)3 = (0,5)2/(r2)3
(r2)3 = (1,6 x 1011)3 (0,52/12)
(r2) = ∛1,24 x 1033
3. Planet A dan B sama-sama berputar mengelilingi matahari. Perbandingan jarak planet A dan B adalah 1:6. Jika planet A mengelilingi matahari selama 90 hari, maka berapa waktu tempuh dari planet B?
Pembahasan:
Diketahui:
ra : rb = 1:6
TA = 90 hari
Ditanyakan: TB?
Jawab:
k = T2/r3
k = TA2/rA3 = TB2/rB3
k = (90)2/(1)3 = TB2/(6)3
TB = √(6)3 x (90)2
TB = 36 x 90 = 3240 hari
4. Waktu yang dibutuhkan Pluto untuk berputar mengelilingi matahari adalah selama 2 tahun, dengan jarak tempuh sebesar 1,5 x 1011 Apabila waktu yang dibutuhkan planet Saturnus untuk berputar mengelilingi matahari adalah selama 1 tahun, berapakah jarak antara planet Saturnus dengan Matahari?
Baca Juga : Gelombang Elektromagnetik
Pembahasan:
Diketahui:
Tp= 2 tahun
rp= 1,5 x 1011 m
TS = 2 tahun
Ditanyakan: rS?
Jawab:
(Tp)2/(rp)3 = (TS)2/(rS)3
(1,5)2/(1,5 x 1011)3 = (2)2/(rS)3
(rS)3 = (1,5 x 1011)3 (22/1,52)
(r2) = ∛6,008 x 1033
5. Jika ada planet A dan B sedang mengorbit matahari. Maka perbandingan antara jarak planet A dan B ke matahari (RA : RB = 1 : 4). Namun, jika periode planet A mengelilingi matahari ialah 88 hari maka periode planet B menjadi berapa hari?
Pembahasan:
Diketahui:
RA : RB = 1 : 4
TA = 88 hari.
Ditanya: Tb?
Jawab:
(Tb/Ta)2= (Rb/Ra)3
(Tb/88)2= (4/1)3
(Tb/88) 2 = 4 x 4 x 4
Tb/88 = √(4 x 4 x 4)
Tb/88 = 2 x 2 x 2
Tb/88 = 8
Tb = 88 x 8
Tb = 704 hari
Demikian artikel pembahasan tentang pengertian hukum kepler, bunyi hukum kepler 1, 2, 3, fungsi, rumus dan contoh soal hukum kepler secara lengkap. Semoga bermanfaat