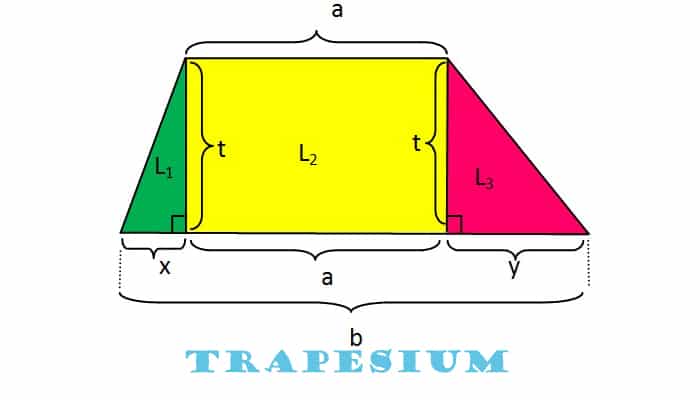
Pengertian, Sifat, Jenis, Rumus dan Contoh Soal Trapesium Beserta Jawaban Lengkap – Trapesium adalah bangun datar dua dimensi tang dibentuk oleh 4 rusuk diantaranta saliung sejajar namun tidak sama panjang.
Sifat TrapesiumCopied!
Adapun sifat dan ciri-ciri trapesium yaitu:
- Memiliki 4 sisi dan 4 titik sudut.
- Memiliki sepasang sisi yang sejajar tapi tidak ama panjang.
- Memiliki sudut di antara sisi sejajarnya sebesar 180°.
Jenis-Jenis TrapesiumCopied!
Ada 3 jenis trapesium yaitu:
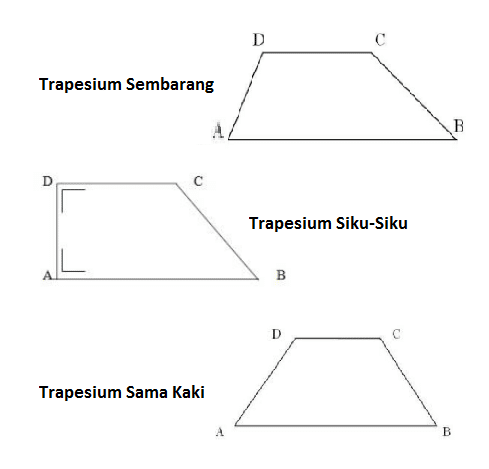
- Trapesium sembarang, trapesium yang keempat rusuknya tidak sama panjang serta tidak memiliki simetri lipat dan hanya memiliki 1 simetri putar.
- Trapesium sama kaki, trapesium yang memiliki sepasang rusuk yang sama panjang, di samping memiliki sepasang rusuk yang sejajar. Trapesium ini memiliki 1 simetri lipat dan 1 simetri putar.
- Trapesium siku-siku, trapesium yangdua di antara keempat sudutnya adalah sudut siku-siku. Rusuk-rusuk yang sejajar tegak lurus dengan tinggi trapesium ini serta tidak memiliki simetri lipat dan hanya memiliki 1 simetri putar.
Rumus TrapesiumCopied!
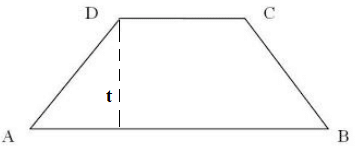
Rumus Luas Trapesium
L = 1/2 x jumlah sisi sejajar x tinggi
Rumus Keliling Trapesium
K = Jumlah seluruh sisi (misalnya AB+BC+CD+DA)
Contoh Soal TrapesiumCopied!
1. Sebuah trapesium mempunyai panjang sisi-sisi sejajar berturut-turut 4 cm dan 10 cm serta tinggi 5 cm. maka, berapakah luas trapesium tersebut?
Cara penyelesaian:
Diketahui:
sisi sejajar: a1 = 4 cm, a2 = 10 cm
t= 5 cm
Ditanya: L…?
Jawab:
L = ½ x (a1 + a2) x t
L = ½ x (4 cm + 10 cm) x 5 cm
L = ½ x 14 x 5
L = 35 cm.
2. Perhatikan gambar di bawah ini!
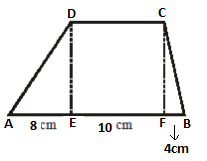
Diketahui, ABCD adalah trapesium dengan CDEF suatu persegi dan EF = 10 cm. Jika AE = 8 cm, FB = 4 cm, AD = 12 cm, dan BC = 10 cm, tentukanlah :
a. panjang CD
b. panjang alas trapesium
c. keliling trapesium ABCD
Cara penyelesaian:
a. Perlu diingat bahwa salah satu sifat persegi yaitu pada tiap sisinya sama panjang, maka panjang CD = EF = 10 cm.
b. Untuk mengetahui panjang alas trapesium (AB) dapat diketahui dengan menjumlahkan:
AB = AE + EF + FB
AB = 8 cm + 10 cm + 4 cm
AB = 22 cm.
c. Keliling trapesium dapat diketahui dengan cara menjumlahkan seluruh sisinya:
K = AB + BC + CD + AD
K = 22 cm + 10 cm + 10 cm + 12 cm
K = 54 cm.
3. Pak Ade mempunyai tanah kosong yang berbentuk trapesium. Panjang sisi tanah yang sejajar adalah 10 meter dan 16 meter dan luasnya 156 m2. Berapakah lebar tanah pak Ade tersebut?
Cara penyelesaian:
Diketahui:
a = 10 m
b = 16 m
L = 156 m2
Ditanya: Lebar tabah?
Jawab:
t = 2L : (a + b)
t = 2.156 : (10 + 16)
t = 312 : 26
t = 12
Jadi lebar tanah pak Ade adalah 12 meter.
4. Salah satu sisi atap rumah pak Budi berbentuk trapesium. Panjang sisi bawah adalah 8 meter dan panjang sisi atas adalah 5 meter. Jika tinggi trapesium tersebut 4 meter, berapakah luasnya?
Cara penyelesaian:
Diketahui:
a = 8 m
b = 5 m
t = 4 m.
Ditanya: L..?
Jawab:
L = ½ (a + b) × t
L = ½ (8 + 5) × 4
L = ½.13 × 4
L = 6,5 × 4
L = 26 m2
Jadi luas atap rumah pak Budi adalah 26 m2.
5. Diketahui luas trapesium 104 cm2. Panjang sisi sejajar 15 cm dan 11 cm. berapakah tinggi trapesium tersebut ?
Cara penyelesaian:
Diketahui:
a = 15 cm
b = 11 cm,
L = 104 cm2
Ditanya: t…?
Jawab:
t = 2L : (a + b)
t = 2.104 : (15 + 11)
t = 208 : 26
t = 8
Jadi tinggi trapesium di atas adalah 8 cm.
6. Pak Maman baru saja selesai mengecat tembok rumahnya yang berbentuk trapesium. Tinggi tembok tersebut yaitu 3,5 meter, sedangkan panjang sisi atas tembok adalah 5 meter. Jika luas tembok 22,75 m2, berapakah panjang sisi alas ?
Cara penyelesaian:
Diketahui:
t = 3,5 m
a = 5 m
L = 22,75 m2
Ditanya: b…?
b = (2L : t) – a
b = (2.22,75 : 3,5) – 5
b = 13 – 5
b = 8
Jadi panjang sisi alasnya adalah 8 m.
7. Pak Bambang sedang memasang genting di bagian atas teras rumahnya. Atap terasnya berbentuk trapesium. Genting tersebut disusun sebagai berikut. Baris pertama atau paling atas sebanyak 20 genting. Baris terakhir atau paling bawah sebanyak 34 genting dan susunan genting terdiri atas 15 baris. Jika kalian disuruh pak Bambang untuk menghitungnya, berapa banyak genting di atap teras Pak Bambang?
Cara penyelesaian:
Diketahui:
a = 20
b = 34
t = 15.
Ditanya: banyak genting di atap teras?
Jawab:
L = ½ (a + b) × t
L = ½ (20 + 34) × 15
L = ½.54 × 1
L = 27 × 15
L = 405.
Jadi banyak genting diatap teras Pak Bambang adalah 405 genting.
8. Pak Andi sedang membuat petak kecil untuk membuat benih padi. Petak tersebut berbentuk trapesium siku-siku. Jarak sisi yang sejajar adalah 5m. kedua sisi-sisi yang sejajar tersebut berukuran 4 m dan 6 m. berapakah luas petak yang dibuat oleh pak Andi ?
Cara penyelesaian:
Diketahui:
t = 5 m
a = 4 m
b = 6 m
Ditanya: L…?
Jawab:
L = ½ (a + b) × t
L = ½ (5 + 4) × 6
L = ½.9 × 6
L = 4,5 × 6
L = 27 m2
Jadi luas petak yang dibuat oleh pak Andi adalah 27 m2.
9. Jika diketahui sebuah trapesium dengan tinggi 15 cm. dan panjang sisi sejajarnya adalah 16 cm dan 24 cm. berapakah luas trapesium tersebut ?
Cara penyelesaian:
Diketahui:
t = 15 cm
a = 16 cm
b = 24 cm.
Ditanya: L..?
Jawab:
L = ½ (a + b) × t
L = ½ (16 + 24) × 15
L = ½.40 × 15
L= 20 × 15 = 300 cm2
Jadi luas dari bangun trapesium di atas adalah 300 cm2.
10. Perhatikan pernyataan trapesium dan layang-layang berikut ini.
- Trapesium dengan tinggi 12 cm dan panjang sisi sejajarnya 18 cm dan 24 cm.
- Layang-layang dengan dengan panjang diagonalnya adalah (10 + 10) cm dan (16 + 8) cm.
Diantara kedua bangun di atas, bangun manakah yang lebih luas ?
Cara penyelesaian:
Diketahui trapesium:
a = 18 cm
b = 24 cm
t = 12 cm.
Ditanya: L…?
Jawab:
L = ½ (a + b) × t
L = ½ (18 + 24) × 12
L = ½.42 × 12
L = 21 × 12
L = 252 cm2
Jadi luas trapesium adalah 252 cm2.
Diketahui layang-layang:
d1 = (10 + 10) cm
d2 = (16 + 8) cm
Ditanya: L..?
Jawab:
L = ½ × d1 × d2
L = ½ × (10 + 10) × (16 + 8)
L = ½ × 20 × 24
L = ½ × 480
L = 240
Jadi luas layang-layang di atas adalah 240 cm2.
Kesimpulannya yaitu lebih luas bangun trapesium, dengan luas 252 cm2.
11. Diketahui bangun layang-layang dengan panjang diagonal yaitu 30 cm dan 26 cm serta bangun trapesium dengan panjang sisi sejajar yaitu 30 cm dan 40 cm. Jika luas kedua bangun tersebut sama, berapakah tinggi bangun trapesium tersebut?
Cara penyelesaian:
Diketahui:
d1 = 30 cm,
d2 = 26 cm,
a = 30 cm
b = 40 cm.
Jawab:
L layang-layang= ½ × d1 × d2
L = ½ × 30 × 26
L = ½ × 780
L= 390.
Jadi luas bangun trapesium adalah 390 cm2.
t trapesium= 2L : (a + b)
t = 2.390 : (30 + 40)
t = 780 : 70
t = 11,1
Jadi tinggi trapesium yaitu 11,1 cm.
12. Pada hari minggu pagi warga di desa pak Bambang melakukan suatu kerja bakti. Warga mengecat atap gapura yang berbentuk trapesium pada sisi depan dan belakang. Atap gapura tersebut memiliki panjang sisi sejajarnya yaitu 4 m dan 3 m dan jarak kedua sisi tersebut 0,9 m. berapakah luas atap gapura yang dicat oleh warga ?
Cara penyelesaian:
Diketahui:
a = 4 m
b = 3 m
t = 0,9 m.
Ditanya: L..?
Jawab:
L = ½ (a + b) × t
L = ½ (4 + 3) × 0,9
L = ½.7 × 0,9
L = 3,5 × 0,9
L = 3,15 m.
Jadi luas atap gapura yang dicat oleh warga adalah 3,15 m2.
Demikian penjelasan yang bisa kami sampaikan tentang Pengertian, Sifat, Jenis, Rumus dan Contoh Soal Trapesium Beserta Jawaban Lengkap . Semoga bermanfaat dan sampai jumpa pada postingan selanjutnya.
Originally posted 2023-05-07 16:51:44.