Balok – Sifat-Sifat Balok, Unsur-Unsur Balok, Rumus dan Contoh Soal Balok Beserta Cara Penyelesaian – Balok adalah bangun ruang 3 dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang dengan paling tidak ada sepasang diantaranya berukuran berbeda. Balok memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Balok memiliki sifat, unsur, dan juga rumus seperti luas permukaan, volume, bidang diagonal, diagonal bidang, dan diagonal ruang.
Sifat-Sifat Balok
- Sisi-sisi balok berbentuk persegi panjang.
- Rusuk-rusuk yang sejajar memiliki ukuran sama panjang.
- Setiap diagonal bidang pada sisi yang berhadapan memiliki ukuran sama panjang.
- Setiap diagonal ruang pada balok memiliki ukuran sama panjang.
- Setiap bidang diagonal pada balok memiliki bentuk persegipanjang.
Unsur-Unsur balok
Sisi atau Bidang
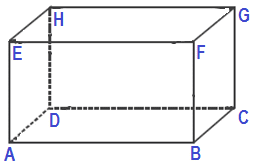
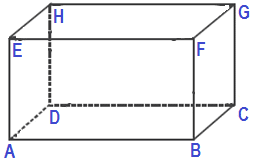
Sisi balok adalah bidang yang membatasi balok. Balok memiliki 6 sisi. Perhatikan gambar diatas yang merupakan yang merupakan sisi adalah sisi bawah (ABCD); sisi atas (EFGH); sisi depan (ABFE); sisi belakang (DCGH);sisi samping kiri (BCGF); dan sisi samping kanan(ADHE).
Balok memiliki 3 pasang sisi yang sama bentuk dan ukurannya. Pasangan tersebut adalah:
Sisi ABFE = sisi DCGH
Sisi ABCD = sisi EFGH
Sisi BCGF = sisi ADHE.
Rusuk
Rusuk adalah garis potongan antar dua sisi bidang balok dan terlihat seperti kerangka yang menyusun balok. Sama seperti kubus, balok memiliki 12 rusuk . Perhatikan gambar kubus diatas yang merupakan rusuk adalah AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, dan HD.
Titik Sudut
Titik Sudut adalah titik potongan antara dua atau 3 rusuk. Balok memiliki 8 titik sudut. Perhatikan gambar diatas, yang merupakan titik sudut yaitu A, B, C, D, E, F, G, dan H.
Diagonal Bidang atau Diagonal Sisi
Diagonal Bidang atau Diagonal Sisi adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan pada setiap bidang atau sisi balok. Sama halnya dengan kubus, balok memiliki 12 Diagonal bidang. Perhatikan gambar diatas, yang merupakan diagonal bidang yaitu AF, BE, BG, CF, CH, DG, DE, AH, AC, BD, EG, dan HF.
Diagonal Ruang
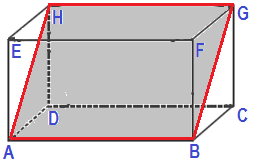
Diagonal Ruang adalah garis yang menghubungkan 2 titik sudut yang saling berhadapkan dalam satu ruang. Sama halnya dengan kubus, balok memiliki 4 diagonal ruang. Perhatikan gambar diatas, yang merupakan diagonal ruang yaitu AG , BH , CE , dan DF.
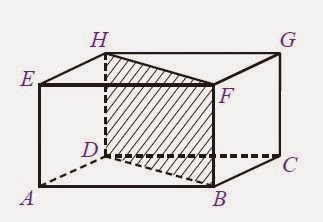
Bidang Diagonal
Bidang diagonal adalah bidang yang dibatasi oleh dua rusuk dan dua diagonal bidang. Sama halnya dengan kubus, balok memiliki 6 bidang diagonal. Perhatikan gambar diatas, yang merupakan bidang diagonal yaitu ACGE, AFGD, CDEF, BFHD, dan BEHC.
Rumus Balok
Luas permukaan
L : 2.(p.l+p.t+l.t)
Volume
V : p.l.t
Panjang diagonal ruang
Dr : √(p2+l2+t2)
Panjang Diagonal Bidang
Db1 : √(s2+s2)
Db2 : √(s2+s2)
Db3 : √(s2+s2)
Luas Bidang Diagonal
Lb1 : Db1.t
Lb2 : Db2.l
Lb3 : Db3.p
Contoh Soal
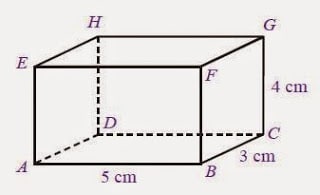
1. Diketahui sebuah balok berukuran sebagai berikut!
a. Tentukan luas permukaan balok!
b. Tentukan Volume balok!
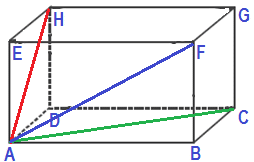
2. Perhatikan gambar balok dibawah ini!
Diketahui panjang AB= 12 cm, BC = 8 cm dan AE = 5 cm. Hitunglah:
a. Panjang AF
b. Panjang AC
c. Panjang AH
a). Panjang AF dapat dihitung dengan teorema phytagoras. Perhatikan segitiga ABF siku-siku di B, maka:
AF = √(AB2 + BF2)
AF = √(122 + 52)
AF = √(144 + 25)
AF = √169
AF = 13 cm
b). Perhatikan segitiga ABC siku-siku di B, maka:
AC = √(AB2 + BC2)
AF = √(122 + 82)
AF = √(144 + 64)
AF = √208
AF = 4√13 cm
c). Perhatikan segitiga AEH siku-siku di E, maka:
AC = √(AE2 + EH2)
AF = √(52 + 82)
AF = √(25 + 64)
AF = √89 cm
3. Sebuah balok memiliki panjang 12 cm, lebar 8 cm dan tinggi 4 cm. Hitunglah berapa panjang diagonal ruang balok?
4. Perhatikan gambar balok di bawah berikut ini!
Diketahui panjang AB = 12 cm, BC = 8 cm dan AE = 6 cm. Hitunglah luas bidang diagonal ABGH!
Terlebih dahulu harus cari panjang BG dengan teorema phytagoras.
BG = √(BC2 + CG2)
BG = √(82 + 62)
BG = √(64 + 36)
BG = √100
BG = 10 cm
Luas bidang diagonal ABGH dapat dicari dengan rumus persegi panjang, yaitu:
Luas ABGH = AB . BG
Luas ABGH = 12 cm . 10 cm
Luas ABGH = 120 cm2
Demikian penjelasan yang bisa kami sampaikan tentang Balok – Sifat-Sifat Balok, Unsur-Unsur Balok, Rumus dan Contoh Soal Balok Beserta Cara Penyelesaian . Semoga bermanfaat dan sampai jumpa pada postingan selanjutnya.