Rumus Dan Contoh Soal Polinom atau Suku Banyak Dalam Matematika
Perhatikan masalah yang di hadapi seorang peneliti sedang merancangsebuah wadah berbentuk balok dari bahan alumunium. Wadah tersebut harus mampu menampung 4.000 ml larutan. Peneliti mengingikan lebar wadah 5 cm lebih pendek dari panjangnya dan tinggi wadah 17 cm lebih pendek dari panjangnya. Dengan memisalkan panjang wadah x cm diperoleh persamaan x3 – 22x2 + 85x – 4.000 = 0. Dapatkah anda menentukna nilai x yang memenuhi persamaan tesebut?
Persamaan x3 – 22x2 + 85x – 4.000 = 0 merupakan persamaan suku banyak. Kali ini kita akan membahas materi tentang suku banyak.
Pengertian Suku Banyak
Suku abnyak atau sering disebut dengan polinom merupakan bentuk suku suku dengan nilai banyak yang disusun dari perubah variabel dan konstanta. Operasi yang digunkana hanya penjumlahan, pengurangan, perkalian dan pangkat bilangan bulat tak negative.
Bentuk umum suku banyak
Bentuk umum suku banyak (polinom) berderajat n dengan variable x adalah:
an xn + an-1 xn-1 + . . . + a1 x + a0
dengan an , an-1 , …. , a1 , a0 € R koefisien/konstanta
suku banyak an ≠ 0 , dan n bilangan bulat positif.
Pangkat tertinggi dari x adlah derajat suku banyak, sedangkan suku yang tidak memuat variable (a0) dinamakna suku tetap (konstan).
Nilai suku banyak
Nilai suku banyak f(x) untuk x=k atau f(k) dapat ditentukan dengan substitusi atau dengan skema Horner
- Cara subtitusi
Dengan mensubtitusikan x = k ke suku banyak
f(x) = an xn + an-1 xn-1 + . . . + a1 x + a0
f(x) = an kn + an-1 kn-1 + . . . + a1 k + a0
- Cara skema horner
Misalkan f(k) = ax3 + bx2 + cx + d maka f(k) = ak3 + bk2 + ck + d
ax3 + bx2 + cx + d = (ak2 + bk + c)k+d
= ((ak + b)k + c)k+d
Diketahui suku banyak p(x) = 2x4 + x2 – 4x + 6
a. Tentukan derajat, koefisien-koefisien dan suku tetap dari suku banyak p(x)
b. Tentukan nilai suku banyak p(x) untuk x=-1
Jawab
a. P(x) = 2x4 + x2 – 4x + 6
= 2x4 + 0x3 + 1x2 +(-4)x + 6
Derajat suku banyak adalah 4
Koefisien x4 adalah 2
Koefisien x3 adalah 0
Koefisien x2 adalah 1
Koefisien x adalah -4
Suku tetap adalah 6
b. P(x) = 2x4 + x2 – 4x + 6
P(-1) = 2(-1)4 + (-1)2 – 4(-1) + 6
= 2 + 1+ 4 + 6
= 13
Jadi nilai suku banyak p(x) untuk x=-1 adalah 13
Pembagian suku banyak
Secara umum dapat dituliskan sebagai berikut
f(x) = g(x) h(x) + s(x)
Dengan
f(x) = suku banyak yang dibagi
g(x) = suku banyak pembagi
h(x) = suku banyak hasil bagi
s (x) = suku banyak sisa
Pembagian suku banyak dengan cara horner
Pembagian suku banyak f(x) oleh (x-k) dapat dilakukan dengan cara horner.
Perhatikan pembagian suku banyak (2x2 – 3x2 + x + 6) oleh (x+2) berikut.
F(x) = 2x2 – 3x2 + x + 6
G(x) = x + 2 = x – (-2) -> k = -2
Skema horner
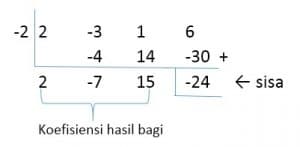
Diperoleh :
Hasil bagi = 2x2 – 7x + 15
Sisa = -24
Jadi, dapat dituliskan :
2x3 – 3x2 + x + 6 = (x+2) (2x2 – 7x + 15) + (-24)
Teorema sisa dan teorema factor
Bagaimana cara menentukan akar persamaan dengan panmgkat lebih dari dua? Sekarang akan kita pelajari selengkapanya, yaitu dengan menggunakan teorema sisa dan teorema factor.
a. Teorema sisa
Jika suku banyak f(x) dibagi x – k maka sisanya adalah f(x).
Sifat
Sisa pembagian suku banyak f(x) oleh ax + b adalah
![]()
Sisa pembagian suku banyak f(x) oleh (x-a) (x-b) adalah
![]()
b. Teorema faktor
Suku banyak f(x) mempunyai factor (x-k) jika dan hanya jika f(x) = 0; k disebut juga akar dari f(x).
Persamaan suku banyak berbentuk an xn + an-1 x n-1 + . . . + a0 dan (x-k) adalah factor dari f(x), maka nilai k yang mungkin adalah
![]()
Diketahui sisa pembagian suatu suku banyak f(x) oleh ( x2 + 6x – 16) adalah (4x-5). Tentukan :
a. Sisa pembagian suku banyak f(x) oleh (x-2) ;
b. Nilai f(-8).
Jawaban:
Jika h(x) hasil bagi dan s(x) = 4x-5 merupakan sisa pembagian, dapat dituilskan:
F(x) (x2+6x – 16) h(x) + s(x)
=( x + 8) (x-2) h(x) + (4x-5)
a. Sisa pembagian f(x) oleh (x – 2):
S(2) = 4(2) – 5
= 8 – 5 = 3
b. f(x) = (x + 8) (x – 2) h(x) + (4x -5)
f(-8) = (-8 +8) (-8 -2) h(-8) + (4(-8) -5)
= (0) (-10) h(-8) + (-32 -25)
= 0 + (-37) =-37
Atau dengan teorema sisa diperoleh:
f(-8) = s(-8) = 4(-8) – 5
= -32 – 5
= -37
Jadi, f(-8) = -37
Demikian penjelasan yang bisa kami sampaikan tentang Rumus Dan Contoh Soal Polinom atau Suku Banyak Dalam Matematika. Semoga postingan ini bermanfaat bagi pembaca . Sampai jumpa pada postingan selanjutnya.