Dinamika Gerak Rotasi : Pengertian, Rumus Dan Pembahasan Contoh Soal – Aksi akrobat selalu menghadirkan decak kagum setiap orang yang menyaksikan. Atraksi yang sering dilakukan misalnya melipat tubuh dan menaiki roda yang dijalankan di atas tali. Para pemain akrobat dapat dengan mudah mengendarai sebuah sepeda meskipun para pemain bertumpuk-tumpuk di atas sepeda. Hal tersebut tidak mudah dilakukan karena melibatkan berbagai gaya berat dari para pemain dan pengaturan posisi setiap pemain sehingga terjadi kesetimbangan rotasi. Dapatkah Anda menjelaskan kesetimbangan tersebut? Pelajari pada artikel ini dengan saksama sehingga Anda dapat menjawab pertanyaan tersebut.

Mengenal Gerak Rotasi
Benda dapat melakukan berbagai jenis gerakan. Benda dapat bergerak lurus dan berpindah tempat. Gerakan semacam ini disebut gerak translasi. Benda juga dapat melakukan gerakan berputar (rotasi). Gerak rotasi yaitu gerakan memutar dari suatu benda terhadap titik tertentu. Sebagai contoh yaitu gerak rotasi gasing. Pada gasing, titik yang menjadi acuan perputaran yaitu ujung tumpuan saat gasing berputar. Apa saja besaran yang terlibat dalam gerak rotasi? Besaran-besaran yang terlibat dalam gerak rotasi sebagai berikut
1. Torsi (Momen Gaya)
Besaran yang menyebabkan terjadinya gerak rotasi adalah torsi. Besaran ini disimbolkan dengan T. Torsi merupakan hasil kali antara gaya dengan lengannya. Adapun lengan gaya merupakan jarak tegak lurus antara sumbu rotasi dengan garis kerja gaya.
Secara matematis, torsi dirumuskan sebagai berikut
τ = r F sin Ѳ
Keterangan:
r = lengan gaya (meter)
F = gaya (newton)
τ = momen gaya torsi (Nm)
e = sudut antara r dan F
2. Momen Inersia
Massa benda merupakan ukuran kelembaman benda pada gerak lurus (gerak translasi). Dengan menganalogikan hal tersebut, diperoleh besaran yang menentukan kelembaman benda pada gerak rotasi. Besaran tersebut dinamakan momen inersia yang disimbolkan dengan /dan dirumuskan sebagai berikut.
|= m r2
Keterangan:
|= momen inersia (kg m2)
m = massa benda (kg)
r = lengan gaya (meter)
Nilai Momen Inersia untuk sistem benda dengan jumlah lebih dari satu sebagai berikut.
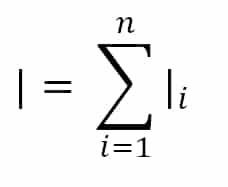
Pada hukum II Newton, hubungan antara gaya, massa, dan percepatan benda dirumuskan sebagai berikut.
F= ma
Gaya tersebut merupakan penyebab terjadinya gerak translasi, massa (m) merupakan ukuran kelembaman gerak translasi, dan percepatan linear (a) merupakan percepatan yang timbul pada gerak translasi.
Anda telah mengetahui bahwa torsi merupakan penyebab gerak rotasi dan momen inersia (/) merupa-kan ukuran kelembaman pada gerak rotasi. Adapun percepatan yang timbul pada gerak rotasi dinamakan percepatan sudut (a). Dengan demikian, hukum II Newton untuk gerak rotasi dirumuskan sebagai berikut.
τ = | α
Keterangan:
τ =torsi (Nm)
| = momen inersia (kg m2)
α= percepatan sudut (rad/s2)
3. Momentum Sudut
Momentum sudut (L) mempunyai persamaan dengan momentum linear (p). Momentum linear merupakan hasil kali antara massa dengan kecepatan benda. Adapun momentum sudut adalah hasil kali antara momen inersia dengan kecepatan sudut benda saat berputar. Secara matematis momentum sudut dirumuskan sebagai berikut.
L= | ω
Keterangan:
| = momen inersia (kg m2)
ω = kecepatan sudut (rad/s)
L = momentum sudut (kg m2/s)
4. Gerak Rotasi Menurut Hukum II Newton
Hukum II Newton untuk gerak rotasi dapat dinyatakan dalam rumus berikut.
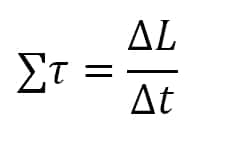
Menurut rumusan tersebut dapat dipahami bahwa perubahan torsi yang terjadi pada suatu benda merupakan laju perubahan momentum sudutnya.
Selain rumusan di atas gerak rotasi menurut hukum II Newton dapat dinyatakan sebagai berikut.
∑τ = │α
5. Hukum Kekekalan Momentum Sudut
Konsep hukum ini sebagai berikut.
“Jika torsi yang bekerja pada benda bernilai nol, momentum sudut total benda yang berotasi besarnya tetap (konstan)”. Persamaan yang terkait dengan hukum ini yaitu:
∆L = 0
L0 = L1 = L2 = … … … = LN = konstan
| ω0 = | ω1 = | ω2 = … … … =| ωN = konstan
6. Hukum Kekekalan Energi pada GerakTranslasi dan Rotasi
Rumusan energi kinetik translasi:
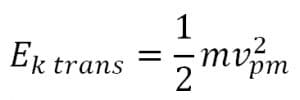
Rumusan energi kinetik rotasi:
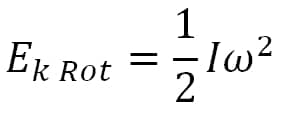
Energi kinetik total dan benda:
![]()
Energi total atau energi mekanik dirumuskan:
![]()
Contoh Soal !
Baling-baling kipas angin berputar 25 rad/s. Jika momen inersia kipas angin 0,002 kg m2, tentukan momentum sudut kipas angin tersebut!
Penyelesaian:
Diketahui:
I= 0,002 kg m2
ω = 25 rad/s
Ditanyakan: L
Jawab:
L = I ω
= (0,002 kg m2)(25 rad/s)
= 0,05 kg m2/s
Demikian penjelasan yang bisa kami sampaikan tentang Dinamika Gerak Rotasi : Pengertian, Rumus Dan Pembahasan Contoh Soal. Semoga postingan ini bermanfaat bagi pembaca dan bisa dijadikan sumber literatur untuk mengerjakan tugas. Sampai jumpa pada postingan selanjutnya.
Baca postingan selanjutnya:
- Teorema Usaha Dan Energi – Pengertian Dan Rumus Usaha, Energi, Dan Daya
- Gerak Harmonik, Pengertian, Rumus Dan Bentuk Gerak Harmonik Sederhana
- Elastisitas Fisika – Pengertian, Rumus, Hukum Hooke, Dan Contoh Soal
- Bunyi Hukum Kepler I , II, III dan Kelajuan Satelit Mengorbit Planet.
- Hukum Newton tentang Gravitasi : Gaya Gravitasi, Medan Gravitasi, dan Energi Potensial Gravitasi
- Gerak Parabola, Pengertian, Rumus, Dan Pembahasan Contoh Soal Gerak Parabola