Pengertian, Rumus, Cara Menghitung Panjang Busur, Luas Juring Dan Luas Tembereng Lingkaran Terlengkap – Pada sebuah lingkaran terdapat bagian yang disebut dengan busur, juring, dan tembereng. Busur adalah besaran pokok panjang, sedangkan juring dan tembereng adalah besaran turunan yang berupa luasan. Pada pembahasan kali kita akan membahaas tentang cara menghitung panjang tali busur dan luas juring dan luas tembereng pada lingkaran.
Rumus Panjang Tali Busur, Luas Juring Dan Luas Tembereng Lingkaran
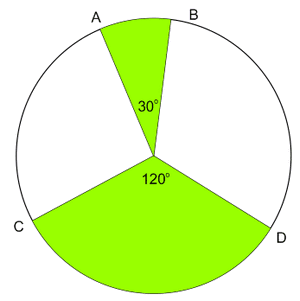
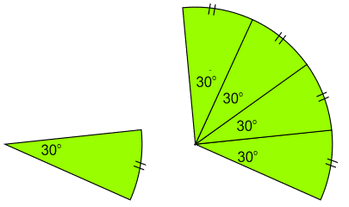
Perhatikan gambar di atas, berdasarkan lingkaran tersebut terdapat dua buah juring, antara lain yaitu AOB dengan sudut AOB = 30º dan juring kedua COD dengan sudut COD = 120º. Bila kemudian kalian mempraktekkannya dengan menggunakan kertas lalu memotong juring AOB dan COD maka akan diperoleh kesimpulan luas juring COD sama dengan 4 kali luas juring AOB.
Jadi, dapat disimpulkan bahwa panjang busur CD = 4 kali panjang busur AB sehingga bisa dibuat perbandingan rumus sebagai berikut :
- Besar sudut AOB : Besar sudut COD = 1 : 4
- Panjang Busur AB : Panjang Busur CD = 1 : 4
- Luas Juring AOB : Luas Juring COD = 1 : 4
Dari hasil perbandingan diatas kita kemudian dapat menyimpulakan bahwa:
Rumus Panjang Tali Busur
Panjang Busur AB = Sudut Pusat / 360º x Keliling Lingkaran.
Panjang Busur AB = α/360º x 2 π r.
Dimana α merupakan sudut pusat, sudut yang menghadap ke tali busur.
Rumus Luas Juring
Luas Juring AOB = Sudut Pusat / 360º x Luas Lingkaran
Luas Juring AOB = α/360º x π r2
Rumus Luas Tembereng
Luas Tembereng = Luas Juring – Luas Segitiga Sama Kaki
Contoh Soal Panjang Busur, Luas Juring Dan Luas Tembereng Lingkaran
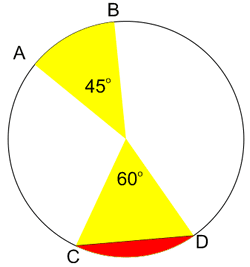
Perhatikan gambar lingkaran di atas, apabila panjang busur AB = 33 cm dan luas juring COD = 924 cm2, maka tentukanlah:
a. Panjang Busur CD
b. Luar Juring AOB
c. Luas Tembereng CD.
Cara Penyelesaian:
a. Panjang Busur AB/CD = ∠ AOB/∠ COD
Panjang Busur CD = ∠COD/∠AOB x Panjang Busur AB
Panjang Busur CD = 60/45 x 33 = 44 cm.
b. Luas Juring AOB/COD = ∠ AOB/∠ COD
Luas Juring AOB = ∠ AOB/∠ COD x Luas Juring COD
Luas Juring AOB = 45/60 x 924 = 693 cm2.
c. Luas Tembereng CD
Jika kalian perhatikan lagi tentang lingkaran di atas, maka dengan sudut 60º maka panjang OC = OD = CD = jari-jari lingkaran. Untuk mencari jari-jari lingkarannya kalian bisa menggunakan perbandingan sudut untuk mencari keliling lingkaran baru kemudian kalian cari panjang jari-jari nya.
Panjang Busur CD/Keliling lingkaran = 60/360
Keliling lingkaran = Panjang Busur CD x 360/60
Keliling lingkaran = 44 x 6
2 π r = 44 x 6
πr = 132
22/7 x r = 132
r = 132/22 x 7 = 42.
sesudah kalian menemukan r selanjutnya bisa menetukan tinggi segitiga ODC dengan menggunakan dalil phytagoras atau rumus segitiga sama sisi. Kita coba dengan dalil phytagoras
t = √(422-212)
t = √(1,764-441
t = √1.323
t = 21√3
Luas Segitiga ΔOCD = 0,5 x 42 x 21√3
= 441√3
Luas Tembereng CD
= Luas Juring COD – Luas ΔOCD
= (924 – 441√3) cm2.
Demikian penjelasan yang bisa kami sampaikan tentang Pengertian, Rumus, Cara Menghitung Panjang Busur, Luas Juring Dan Luas Tembereng Lingkaran Terlengkap . Semoga bermanfaat dan sampai jumpa pada postingan selanjutnya.
Originally posted 2023-05-22 13:00:17.