Bangun Datar – Apa yang dimaksud dengan bangun datar? Apa yang dimaksud dengan bangun datar dan contohnya? Contoh bangun datar apa saja? Sebutkan jenis-jenis bangun datar?
Baca Juga : Pengertian Bangun Ruang
Agar lebih memahaminya, kali ini kita akan membahas tentang pengertian bangun datar menurut para ahli, nama, jenis, bentuk, contoh dan gambarnya, sifat, rumus serta contoh soal bangun datar secara lengkap.
Pengertian Bangun Datar
Bangun datar adalah sebutan untuk bangun-bangun dua dimensi, gabungan bangun datar dapat membentuk bangun ruang seperti tabung atau yang lainnya.
Pengertian bangun datar adalah bentuk dua dimensi yang dibatasi oleh garis lurus atau garis lengkung.
Bangun datar merupakan bangun berupa bidang datar yang dibatasi oleh beberapa ruas garis. Jumlah dan model ruas garis yang membatasi bangun tersebut menentukan nama dan bentuk bangun datar tersebut. Sebagai contoh, bangun yang dibatasi oleh tiga ruas garis disebut dengan bangun segitiga.
Pengertian ruas garis adalah bagian dari garis yang dibatasi oleh dua titik yang berbeda pada kedua ujungnya, sehingga ruas garis pada bangun datar diartikan sebagai sisi-sisi yang membatasi sebuah bangun datar. Sedangkan, pengertian sisi adalah bidang pada bangun datar yang membatasi antara ruas garis yang satu dengan ruas garis lainnya.
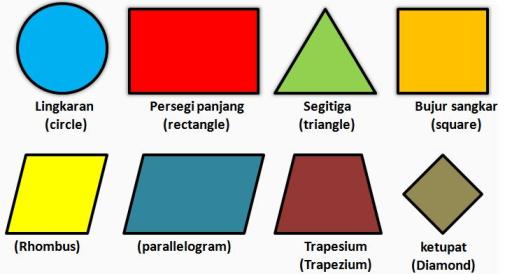
Terdapat macam-macam bangun datar, diataranya persegi panjang, persegi, segitiga, jararan genjang, trapesium, lingkaran, layang-layang dan belah ketupat. Bangun datar yang mempunyai tiga sudut adalah segitiga; bangun datar yang memiliki sisi-sisi sama panjang dan sudut-sudut sama besar (90°) disebut persegi; bangun datar yang mempunyai sisi berhadapan yang sama panjang, dan memiliki empat buah titik sudut siku-siku adalah persegi panjang; bangun ruang berbentuk segi empat yang sisinya sepasang-sepasang sama panjang dan sejajar disebut jajar genjang; bangun datar dengan ruas garis tak terhingga adalah lingkaran; bangun datar yang tidak memiliki sisi disebut bukan segibanyak; dan lain sebagainya. Semua bangun datar memiliki sifat dan rumus yang berbeda.
Pengertian Bangun Datar Menurut Para Ahli
Imam Roji (1997)
Bangun datar adalah bangun dari bidang datar yang dibatasi oleh garis-garis lurus atau lengkung.
Julius Hambali, Siskandar dan Mohamad Rohmad (1996)
Bangun datar adalah bangun yang rata yang mempunyai dua dimensi yaitu panjang dan lebar tapi tidak memiliki tinggi atau tebal.
Elfawati (2012:201)
Bangun datar adalah ilmu yang berhubungan dengan pengenalan bentuk
dan pengukuran.
Rahaju (2008:252)
Bangun datar adalah bangun yang mempunyai dua dimensi yaitu panjang dan lebar tetapi tidak mempunyai tinggi dan tebal.
Sinaga, dkk (2013:300)
Bangun datar yang memiliki empat sisi disebut segiempat sedangkan bangun datar
yang memiliki tiga sisi disebut segitiga.
Jenis-Jenis Bangun Datar
Berikut ini jenis bentuk bangun datar dan gambarnya serta sifat dan rumusnya secara lengkap.
Persegi Panjang
Pengertian Persegi Panjang
Persegi panjang adalah bangun datar yang memiliki sisi berhadapan sama panjang dan memiliki empat titik sudut.
Baca Juga : Rumus Tabung
Sifat Persegi Panjang
Sifat persegi panjang, diantaranya yaitu:
- Memiliki sisi yang berhadapan sama panjang.
- Memiliki empat titik sudut yang sanma besar yaitu 90°
- Memiliki empat dua diagonal yang sama panjang.
- Memiliki 3 simetri lipat.
- Memiliki simetri putar tingkat dua.
Gambar Persegi Panjang
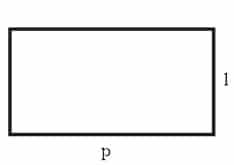
Keterangan:
p = panjang
l = lebar
Rumus Persegi Panjang
Keliling persegi panjang
K = 2. (p+l)
Luas persegi panjang
L = p.l
Panjang diagonal persegi panjang
d = √ p2+l2
Panjang persegi panjang
p = L : l
p = (Keliling : 2) – l
Lebar persegi panjang
l = L : p
l = (Keliling : 2) – p
Persegi
Pengertian Persegi
Persegi adalalah bangun datar yang terbentuk dari empat buah sisi yang sama panjang dan empat sudut yang sama besar 90°.
Sifat Persegi
Adapun sifat-sifat bangun persegi, diantaranya:
- Memiliki dua pasang sisi yang sejajar dan sama panjang.
- Memiliki empat simetri lipat.
- Memiliki simetri putar tingkat empat.
Gambar Persegi
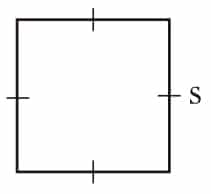
Keterangan:
s = sisi/rusuk
Rumus Persegi
Luas Persegi
L = s2
Keliling Persegi
K = 4s
Sisi Persegi
s = √L
s = Keliling : 4
Panjang Diagonal Persegi
d = √2xs2
Segitiga
Pengertian dan Sifat Segitiga
Segitiga atau segi tiga adalah bangun datar yang dibentuk oleh tiga sisi berupa garis lurus dan memiliki tiga sudut. Selain memiliki 3 sisi atau rusuk dan sudut, sifat yang dimiliki segitiga memiliki besar sudut 180°.
Baca Juga : Rumus Kerucut
Jenis-Jenis Segitiga
Menurut panjang sisinya, terdapat 3 jenis segitiga yaitu:
- Segitiga sama sisi (bahasa Inggris: equilateral triangle) adalah segitiga yang ketiga sisinya sama panjang dan semua sudutnya sama besar yaitu 60°.
- Segitiga sama kaki (bahasa Inggris: isoceles triangle) adalah segitiga yang dua dari tiga sisinya sama panjang dan memiliki dua sudut yang sama besar.
- Segitiga sembarang (bahasa Inggris: scalene triangle) adalah segitiga yang ketiga sisi memiliki panjang dan besar semua sudutnya berbeda.
Menurut besar sudut terbesarnya, segitiga dibagi menjadi 3 jenis yaitu:
- Segitiga siku-siku (bahasa Inggris: right triangle) adalah segitiga yang salah satu besar sudutnya sama dengan 90. Sisi di depan sudut 90° disebut hipotenusa atau sisi miring.
- Segitiga lancip (bahasa Inggris: acute triangle) adalah segitiga yang besar semua sudut < 90°
- Segitiga tumpul (bahasa Inggris: obtuse triangle) adalah segitiga yang besar salah satu sudutnya > 90°.
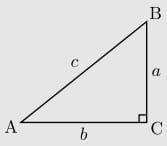
Gambar Segitiga
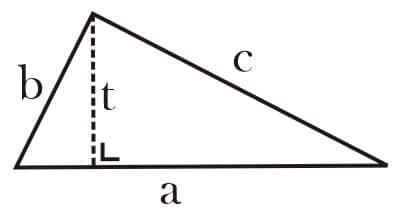
Keterangan:
a = alas
t = tinggi, tinggi segitiga membentuk sudut 90° terhadap alasnya.
b, c = sisi lain segitiga
Rumus Segitiga
Luas Segitiga
L = 1/2.alas.tinggi
Keliling Segitiga
K = sisi x sisi x sisi
Tinggi Segitiga
t = (2 × Luas) : a
Alas Segitiga
a = (2 × Luas) : t
Teorema heron, teorema ini biasnya digunakan untuk mencari luas segitiga sembarang a,b,c adalah ketiga sisi segitiga.
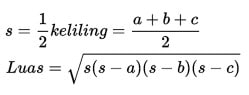
Rumus yang digunakan untuk mencari luas dan keliling segitiga sama sisi yang bersisi a dapat menggunakan rumus berikut ini:
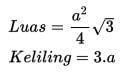
Rumus Pythagoras
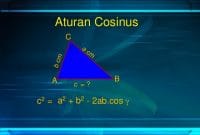
Dalil phytagoras hanya berlaku pada segitiga siku-siku. pythagoras menyatakan bahwa: c2 = a2+b2
Jajar Genjang
Pengertian Jajar Genjang
Jajar genjang atau jajaran genjang adalah bangun datar 2 dimensi yang dibentuk oleh 2 pasang rusuk yang masing-masing sama panjang dan sejajar dengan pasangannya dan memiliki 2 pasang sudut yang sama besar dengan sudut hadapannya.
Baca Juga : Pola Bilangan
Sifat Jajar Genjang
Sifat-sifat jajar genjang, diantaranya yaitu:
- Dibentuk oleh 2 pasang rusuk yang masing-masing sama panjang dan sejajar dengan pasangannya
- Memiliki 2 pasang sudut yang sama besar dengan sudut hadapannya.
- Memiliki 2 diagonal yang berpotonga dalam satu titik dan saling membagi 2 sama panjang.
- Memiliki simetri putar tingkat 2 dan tidak memiliki simetri lipat.
Gambar Jajar Genjang
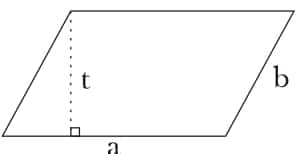
Keterangan:
a = sisi alas
b = sisi miring
t = tinggi
Rumus Jajar Genjang
Luas Jajar Genjang
L = Alas.tinggi
Keliling Jajar Genjang
K = 2. alas + 2. sisi miring.
Sisi Alas Jajar Genjang
a = (Keliling : 2) – b
Sisi Sisi Miring
b = (Keliling : 2) – a
t diketahui L
t = L : a
a diketahui L
a = L : t
Trapesium
Pengertian Trapesium
Trapesium adalah bangun datar dua dimensi yang dibentuk oleh 4 rusuk diantaranya saling sejajar namun tidak sama panjang.
Sifat Trapesium
Sifat-sifat bangun trapesium, diantaranya yaitu:
- Memiliki 4 sisi dan 4 titik sudut.
- Memiliki sepasang sisi yang sejajar tapi tidak ama panjang.
- Memiliki sudut di antara sisi sejajarnya sebesar 180°.
Jenis-Jenis Trapesium
Ada 3 jenis trapesium yaitu:
- Trapesium sembarang, yaitu trapesium yang keempat rusuknya tidak sama panjang serta tidak memiliki simetri lipat dan hanya memiliki 1 simetri putar.
- Trapesium sama kaki, yaitu trapesium yang memiliki sepasang rusuk yang sama panjang, di samping memiliki sepasang rusuk yang sejajar. Trapesium ini memiliki 1 simetri lipat dan 1 simetri putar.
- Trapesium siku-siku, yaitu trapesium yangdua di antara keempat sudutnya adalah sudut siku-siku. Rusuk-rusuk yang sejajar tegak lurus dengan tinggi trapesium ini serta tidak memiliki simetri lipat dan hanya memiliki 1 simetri putar.
Baca Juga : Bilangan Pangkat Pecahan
Gambar Trapesium
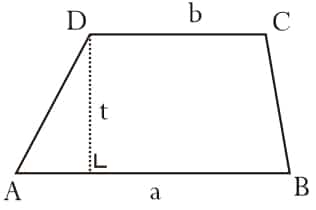
Keterangan:
t = tinggi trapesium
a, b = adalah sisi yang sejajar
Rumus Trapesium
Luas Trapesium
L = 1/2 x jumlah sisi sejajar x tinggi
L = 1/2 x (a+b) x t
atau bisa juga menggunakan rumus:
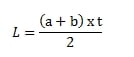
Keliling Trapesium
K = Jumlah seluruh sisi
K = AB + BC + CD + DA
Tinggi Trapesium
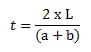
Sisi a (AB)
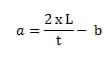atau AB = Keliling – CD – BC – AD
Sisi b (DC)
atau CD = Keliling – AB – BC – AD
Sisi AD
AD = Keliling – CD – BC – AB
Sisi BC
BC = Keliling – CD – AD – AB
Layang-Layang
Pengertian Layang-Layang
Layang-layang adalah bangun datar 2 dimensi yang dibentuk oleh 2 pasang rusuk yang masing-masing pasangan sama panjang dan saling membentuk sudut.
Sifat Layang-Layang
Sifat layang-layang, diantaranya yaitu:
- Mempunyai 2 pasang sisi yang panjang sama.
- Mempunyai satu pasang sudut yang berhadapan yang besarnya sama.
- Mempunyai 4 titik sudut.
- Diagonalnya saling berpotongan tegak lurus.
- Salah satu diagonal bangun ini membagi dua sama panjang diagonal yang lain.
- Hanya mempunyai satu simetri lipat.
Gambar Layang-Layang
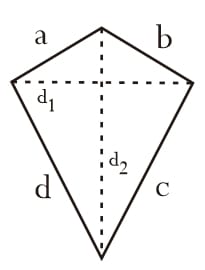
Rumus Layang-Layang
Luas layang-layang
L = ½. d1.d2
Keliling layang-layang
K = 2. (a+c)
K = a+b+c+d
Diagonal 1 layang-layang
d1= 2 × L : d2
Diagonal 2 layang-layang
d2= 2 × L : d1
a atau b
a = (½ × Keliling) – c
c atau d
c = (½ × Keliling) – a
Baca Juga : Pengertian Pengukuran
Belah Ketupat
Pengertian Belah Ketupat
Belah ketupat adalah bangun datar 2 dimensi yang dibentuk oleh 4 rusuk yang sama panjang dan memiliki 2 pasang sudut yang masing-masing sama besar dengan sudut di hadapannya.
Sifat Belah Ketupat
Sifat belah ketupat, diantaranya:
- Memiliki sisi yang sama panjang.
- Sudut-sudut yang berhadapan sama besar serta dibagi dua oleh diagonal dengan sama besar.
- Diagonalnya saling berpotongan sama panjang dan saling tegak lurus.
- Memiliki 2 sumbu simetri.
- Memiliki 2 simetri lipat dan 2 simetri putar.
Gambar Belah Ketupat
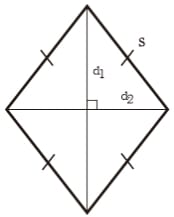
Rumus Belah Ketupat
Luas Belah Ketupat
L = ½. d1.d2
Keliling Belah Ketupat
K = 4.s
K= s + s + s + s
Sisi Belah Ketupat
s = Keliling : 4
Diagonal 1
d1= 2 × L : d2
Diagonal 2
d2= 2 × L : d1
Lingkaran
Pengertian Lingkaran
Lingkaran adalah himpunan semua titik pada bidang dalam jarak tertentu yang disebut dengan jari-jari dari seatu titik yang disebut dengan pusat.
Sifat Lingkaran
Sifat-sifat lingkaran, diantaranya yaitu:
- Mempunyai simetri putar tak terhingga.
- Mempunyai simetri lipat serta sumbu yang tak terhingga.
- Tidak memiliki titik sudut.
- Memiliki satu sisi.
Gambar Lingkaran
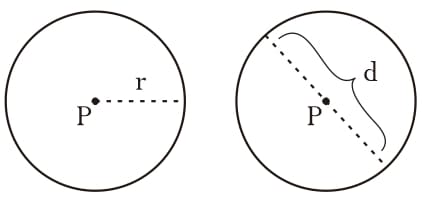
Rumus Lingkaran
Luas Lingkaran
L = π x r x r
L = π x r2
Keliling Lingkaran
K = π x d
K = 2πr
Diameter Lingkaran
d = 2 × r
Jari-jari Lingkaran
r = d : 2
Mencari r Lingkaran
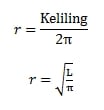
Keterangan:
π = 3,14 atauu 22/7
r = jari-jari
d = diameter (2 x r)
Baca Juga : Hukum Newton (1, 2, 3)
Contoh Soal Bangun Datar
1. Diketahui Layang-layang ABCD, panjang AB = 15 cm dan panjang BC = 20 cm. Tentukan luas dan keliling layang-layang tersebut!
Cara Penyelesaian:
L = ½. d1.d2
= ½ x 15 x 20
= 150 cm2
K = 2. s1 + 2. s2
K = AB + BC + CD +DA
= 15 + 20 + 15 + 20
= 70 cm
2. Diketahui belah ketupat ABCD dengan panjang diagonal masing-masing 18 cm dan 16 cm. Berapakah luas dan keliling tersebut!
Cara Penyelesaian:
L = ½. d1.d2
L= ½ x 18 x 16
= 144 cm2
K = AB + BC + CD + DA
= 18 + 16 + 18 + 16
= 68 cm
3. Jika sebuah segitiga memiliki panjang sisi alas 5 cm dan tinggi sisi 8 cm, maka berapa Luas dan Keliling segitiga tersebut ?
Cara Penyelesaian:
L = ½ x a x t
= ½ x 5 x 8
= 20 cm2
K = a + (2 x b)
= 5 + (2 x 8)
= 21 cm
4. Jika sebuah trapesium memiliki panjang sisi sejajar 12 cm dan 6 cm, tingginya 8 cm. Berapa Luas dan Keliling trapesium tersebut?
Cara Penyelesaian:
L = (a + b) x tinggi : 2
= ((12 + 6) x 8)) : 2
= 72 cm2
K= a + b + c
= 12 + 6 + 8
= 26 cm
5. Diketahui jajar genjang, alasnya 18 cm dan tingginya 6 cm. tentukan luasnya dan kelilingnya!
Cara Penyelesaian:
L = a x t
= 18 x 6
= 108 cm2
K = AB + BC + CD + DA
= 18 + 6 + 18 + 6
= 48 cm
Baca Juga : Hukum Ohm
Demikian artikel pembahasan tentang pengertian bangun datar menurut para ahli, nama, jenis, bentuk, contoh dan gambarnya, sifat, rumus serta contoh soal bangun datar secara lengkap.