Dalam suatu pengukuran, biasanya terdapat kesalahan, atau disebut juga ketidakpastian dalam pengukuran. Kesalahan-kesalahan ini ada yang bisa dihindari, tetapi ada juga yang tidak bisa dihindari. Dalam subbab ini kita akan membahas bentuk-bentuk kesalahan dalam pengukuran dan bagaimana cara menanganinya.
Dua Jenis Pengukuran
Pengukuran dapat dilakukan dengan dua cara, yaitu secara langsung dan secara tidak langsung. Pengukuran secara langsung adalah ketika hasil pembacaan skala pada alat ukur secara langsung menyatakan nilai besaran yang diukur, tanpa perlu dilakukan penambahan, mengambil rata-ratanya, atau pun menggunakan rumus untuk menghitung nilai yang diinginkan. Peng¬ukuran secara tidak langsung memerlukan perhitungan-perhitungan tambahan. Contoh pengukuran langsung adalah menimbang massa sebuah benda dengan neraca, sedangkan contoh pengukuran tidak langsung adalah mengukur luas sebuah persegi panjang. Ketika menimbang, kita langsung membaca berapa massa benda yang ditimbang dalam skala timbangan. Ketika mengukur luas sebuah persegi panjang, kita mengukur panjang dua buah sisi persegi panjang tersebut, untuk selanjutnya menghitung luas persegi panjang dengan rumus sisi dikali sisi.
Presisi dan Akurasi
Dalam pengertian sehari-hari, presisi dan akurasi sering diartikan sebagai dua hal yang memiliki arti sama. Dalam pengukuran, presisi dan akurasi memiliki arti yang berbeda. Presisi dalam sebuah pengukuran bisa dikaitkan dengan 3 hal berikut ini.
- Presisi berkaitan dengan perlakuan dalam proses pengukuran, yang meliputi antara lain kualitas alat ukur, sikap teliti si pengukur, kestabilan tempat di mana dilakukan pengukuran. Contohnya, pengukuran berat badan seorang bayi dengan timbangan bayi lebih presisi dibandingkan dengan pengukuran berat badan bayi tersebut dengan timbangan beras.
- Presisi juga berkaitan dengan seberapa besar penyimpangan hasil ukur suatu besaran ketika pengukuran dilakukan secara berulang-ulang. Sebuah pengukuran yang dilakukan secara berulang memberikan hasil 7,2 cm, 7,3 cm, 7,2 cm, dan 7,3 cm. Pengukuran kedua yang dilakukan oleh orang yang berbeda memberikan hasil 7,2 cm, 7,4 cm, 7,5 cm, dan 7,1 cm. Dapat dikatakan bahwa pengukuran yang dilakukan oleh orang pertama lebih presisi dibandingkan dengan pengukuran yang dilakukan oleh orang kedua.
- Presisi juga berhubungan dengan jumlah angka desimal yang dicantumkan dalam hasil pengukuran. Makin banyak angka desimal dalam suatu hasil pengukuran, makin presisi pengukuran tersebut. Sebagai contoh, hasiJ ukur 3,45 cm lebih presisi dibandingkan dengan 3,5 cm.
Ketiga pengertian presisi tersebut berkaitan satu dengan yang lain, karen proses yang dilakukan dalam pengukuran secara langsung mempengaruli hasil pengukuran yang berulang-ulang. Jadi, presisi berhubungan dengar metode pengukuran dan bagaimana hasil ukur tersebut dituliskan.
Berbeda dengan presisi, akurasi hanya memiliki satu pengertian, yaio seberapa dekat hasil suatu pengukuran dengan nilai yang sesungguhnya Apakah yang disebut nilai yang sesungguhnya ini? Nilai yang sesungguhnya atau sering disebut “angka yang benar” antara lain adalah definisi suati besaran atau konstanta, hukum-hukum geometri, dan angka yang diperole dari suatu teori yang sudah disepakati kebenarannya.
Contoh sederhana mengenai akurasi adalah sebagai berikut. Massa jen air disepakati bemilai 1000 kg/m3. Dua orang siswa melakukan percobaa untuk mengukur massa jenis air. Setelah melakukan beberapa kali pengukura dalam percobaannya, siswa A memperoleh hasil 1002 kg/m3 sedangkan siswa B memperoleh hasil 1005 kg/m3. Dalam kasus ini, kita katakan hasil pengukuran siswa A memiliki akurasi yang lebih tinggi (lebih akurat) diban-i dingkan dengan hasil pengukuran siswa B.
Sebuah pengukuran bisa presisi tetapi tidak akurat, atau akurat tetapi tidak presisi. Sebagai contoh, jika sebuah pengukuran dilakukan dengan metode yang sangat teliti dengan alat ukur yang canggih dan dilakukan berulang-ulang akan menghasilkan pengukuran yang memiliki presisi tinggi. Namun, jika temyata salah satu bagian dari alat ukur tersebut cacat atau tidak berfungsi dengan sempumya, misalnya jarum penunjuk skala bengkoL j maka pengukuran tersebut menjadi tidak akurat.
Hal yang sebaliknya juga bisa terjadi, di mana pengukurannya tidak presisi, tetapi memiliki keakuratan yang tinggi. Contohnya, sebuah pengukuran jarak antara 2 titik dilakukan secara berulang-ulang. Nilai sesungguhnya jarak tersebut telah ditetapkan sebelumnya, yaitu 10 m. Hasil pengukuran yang berulang-ulang memberikan hasil 10,2 m, 9,8 m, 10,8 m, 9,5 m, 10,5 m, dan 9,2 m. Rata-rata hasil pengukuran ini adalah 10 m, tepat dengan nilai yang sesungguhnya, yang berarti pengukurannya akurat. Tetapi, apakah pengukuran yang dilakukan berulang 6 kali tersebut presisi? Tidak, karena terjadi penyimpangan yang cukup besar dalam setiap pengukuran ulang.
Kesalahan (error) dalam Pengukuran dan Sumber-sumbernya
Ketika didefinisikan dengan benar, kesalahan (error) atau ketidakpastian hanya berkenaan dengan pengukuran-yaitu untuk memperkirakan suatu nilai ketika nilai eksak suatu pengukuran tidak mungkin diperoleh. Kesalahan tidak berlaku pada perhitung-an, di mana nilai eksaknya mungkin diperoleh. Sebagai contoh, mengukur tinggi badan seorang anak bisa menghasilkan hasil ukur yang berbeda-beda ketika dilakukan pengukuran berulang-ulang, dan nilai eksaknya pun tidak diketahui secara pasti, sehinsgga hasilnya bisa dinyatakan misalnya sebagai 160 cm plus minus 2 cm. Namun, menghitung jumlah siswa di dalam kelas bisa menghasilkan nilai eksak, misalnya 40 siswa.
Pada dasamya, dalam suatu pengukuran terdapat dua jenis kesalahan, yaitu kesalahan sistematis dan kesalahan random (acak). Sebelum membahas kedua jenis kesalahan ini, akan dibahas lebih dulu sumber-sumber kesalahan.
- Kesalahan alami
Biasanya, suatu pengukuran dilakukan di lingkungan yang tidak dapat dikontrol. Efek suhu, tekanan atmosfer, angin, gravitasi bumi pada alat ukur akan menimbulkan kesalahan-kesalahan pada hasil pengukuran.
- Kesalahan alat
Pengukuran, baik yang dilakukan dengan alat ukur yang sederhana maupun alat ukur yang canggih, tetap saja memungkinkan terjadinya kesalahan, misalnya karena ketidaksampumaan pembuatan alat ukumya di pabrik atau kesalahan kalibrasi.
- Kesalahan manusia
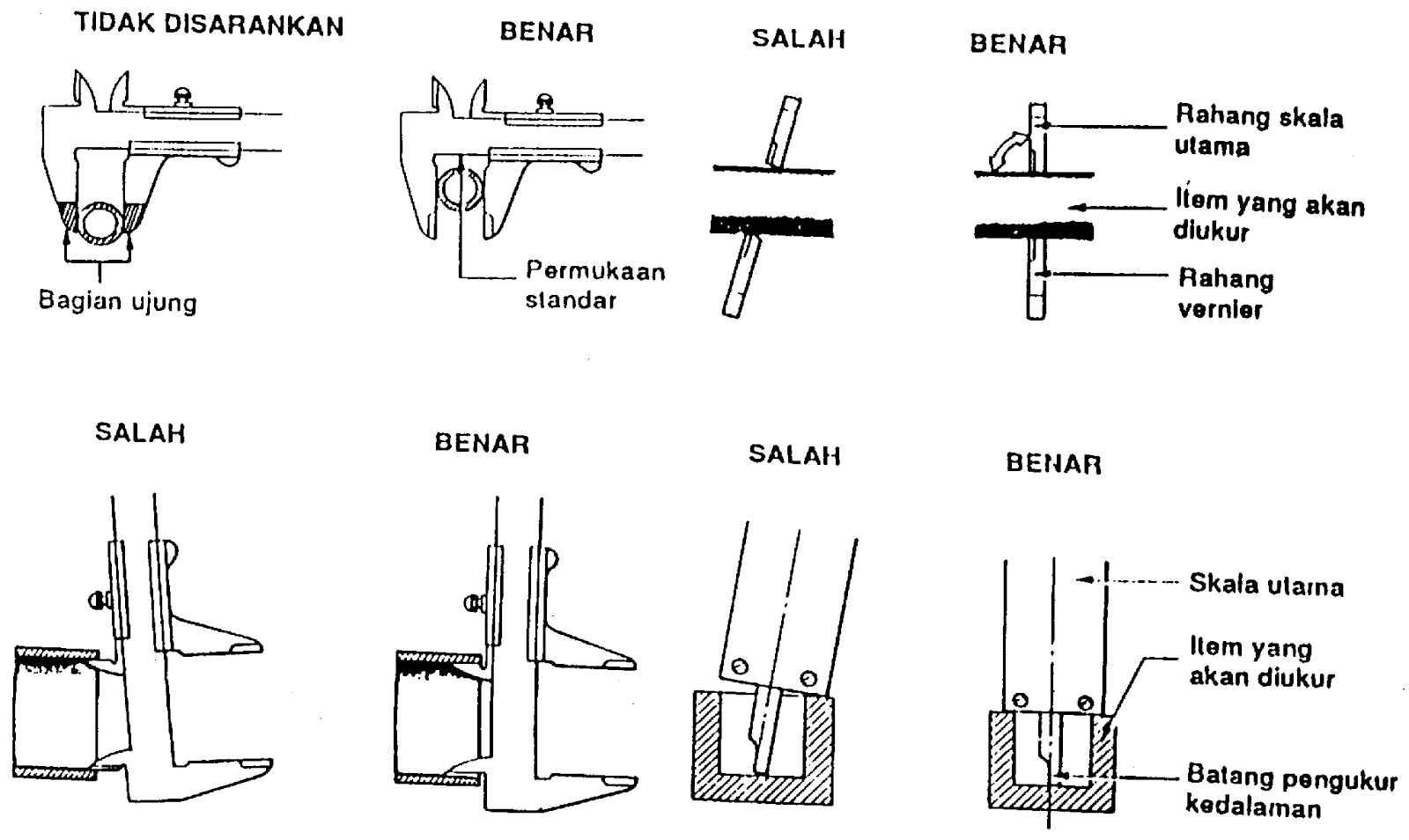
Karena manusia secara langsung terlibat dalam pengukuran, dan cukup banyak unsur subjektif dalam diri manusia, maka kesalahan yang diakibatkan oleh manusia sangat mungkin terjadi dalam pengukuran. Sistem otomatisasi dan digitalisasi telah mengurangi sumber kesalahan yang berasal dari manusia ini. Contoh kesalahan yang ditimbulkan oleh manusia adalah kesalahan paralaks.
- Kesalahan hitung
Kesalahan hitung meliputi cukup banyak hal, misalnya tentang jumlah angka penting yang berbeda-beda dari beberapa hasil pengukuran, kesalahan pembulatan hasil pengukuran, dan penggunaan faktor konversi satuan.
Kesalahan Sistematik
Kesalahan sistematik dalam pengukuran adalah kesalahan-kesalahan yang secara umum berkaitan dengan kesalahan pengaturan alat, kalibrasi alat ukur, atau pengaruh lingkungan tempat di mana pengukuran dilakukan. Contoh kesalahan sistematik adalah ketika meteran plastik yang digunakan tukang bangunan untuk mengukur jarak antara dua titik memanjang karena panas, diameter ban mobil bukan diameter sebenamya yang akan menghasilkan bacaan jarak tempuh pada odometer mobil, dan lain sebagainya. Karena kesalahan sistematik bisa dilacak sumbemya, maka kesalahan sistematik bias dikoreksi atau dikurangi.
Cara untuk mengurangi kesalahan sistematik adalah dengan mendesain pengukuran secara teliti, termasuk misalnya mengisolasi lingkungan di mana percobaan atau pengukuran dilakukan. Tentu saja, kemungkinan terjadinya kesalahan sistematik tetap ada, walaupun percobaan telah dirancang dengan sangat teliti. Cara lain untuk mengurangi kesalahan sistematis adalah dengan melakukan kalibrasi pada alat ukur. Kalibrasi berarti bahwa kita menggunakan alat ukur yang kita miliki untuk mengukur beberapa nilai besaran yang sudah diketahui, kemudian membandingkan hasilnya.
Untuk lebih jelas mengenai kesalahan sistematis ini, simak dengan seksama bagaimana kesalahan sistematis yang timbul dalam pengukuran berat badan dengan timbangan digital berikut ini. Seseorang mungkin menganggap bahwa sebuah neraca digital yang digunakan untuk mengukur berat benda menunjukkan hasil yang sangat eksak karena teknologinya yang sudah digital.
Pada saat belum ada beban, temyata neraca tersebut menunjukkan an: -1,1 gram. Ketika empat buah koin 25-gram ditambahkan satu per sebagai beban, diperoleh hasil pengukuran berturut-turut 24,2, 49,5, 74. dan 100,1 gram. Angka -1,1 gram merupakan kesalahan dari alat yang disel juga sebagai kesalahan tetap. Kita harus menambahkan 1,1 gram untuk seti; hasil penimbangan beban, sehingga hasil penimbangan yang dilakukan h; dikoreksi oleh kesalahan tetap ini, yaitu 25,3, 50,6, 76,0, dan 101,2 gr;
Sampai di sini, kita harus mulai menginterpretasikan data yang peroleh agar bisa kita manfaatkan dengan tepat. Jika kita bagi 50,6 deng; 2, kita peroleh 25,3, angka yang sama dengan hasil penimbangan satu beh Jika kita bagi 76,0 dengan 3, kita peroleh 25,33, hampir sama dengan untuk satu dan dua beban. Dan jika kita bagi 101,2 dengan 4, kita perol 25,3 juga. Jika koin-koin ini dibuat di pabrik dengan ukuran masing-masii 25 gram, maka kita peroleh kesalahan sistematik +0,3 gram, atau +1,2 gr; untuk tiap 100 gram. Kesalahan ini disebut kesalahan sistematik karei mengikuti suatu “sistem” atau “aturan”. Kesalahan ini dapat diprediksi, d; mengikuti suatu aturan matematis, yaitu suatu hubungan linear antara beb; dan kesalahannya. Dalam kasus ini, kesalahan alat sama dengan 1,2/100 = 0,1 per hasil yang ditunjukkan.
Sekarang, berapakah berat (sebenamya massa) yang sesungguhnya d; hasil penimbangan sebuah benda, yang ketika ditimbang menunjukkan ang 144,5 gram? Pertama, kita tambahkan hasil ini dengan kesalahan konst; 1,1 gram, sehingga menjadi 145,6 gram. Hasil ini harus kita kurangi deng; kesalahan sistematisnya yaitu 0,012 x 144,5 = 1,734 gram, sehingga ber; (atau massa) yang sesungguhnya adalah 145,6 – 1,734 = 143,9 gra (dibulatkan).
Kesalahan Random (acak)
Kesalahan random tidak dapat dihindari. Kesalahan random dinyatakan dal tanda plus atau minus. Besar kesalahan random tidak diketahui, tetapi dapat diperkirakan. Kesalahan random disebabkan oleh ketidaksempumaan manusia dan alat, seperti halnya ketidakpastian dalam menentukan pengaruh lingkungan terhadap pengukuran.
Kesalahan personal merupakan kesalahan random. Manusia tidak dapat mengukur dengan sangat tepat. Selalu ada ketidaksempumaan dalam melaku- kan pengukuran, misalnya kesalahan paralaks, kesalahan dalam menentukan letak suatu titik, dan lain sebagainya. Kesalahan random adalah kesalahan yang terjadi ketika kita berusaha melakukan “pengukuran dengan tepat”, tetapi selalu terjadi sedikit salah dalam menentukan apa yang dianggap tepat tersebut karena ketidaksempumaan alat dan manusia sendiri.
Kesalahan random akan selalu muncul, tetapi dapat diperkecil dengan cara melakukan pengukuran berulang-ulang. Selanjutnya, dengan metode statistika, kita dapat menghitung besamya kesalahan random ini. Ketika melaporkan hasil pengukuran, kesalahan (atau ketidakpastian) hasil pengukuran seringkali dinyatakan secara langsung sebagai selisih terbesar antara nilai rata-rata hasil pengukuran dengan masing-masing pengukuran. Di samping itu, kesalahan juga sering dinyatakan sebagai setengah skala terkecil dari alat ukur yang digunakan untuk melakukan pengukuran. Sebagai contoh, perhati- kan hasil pengukuran panjang yang dilakukan 8 kali berikut ini.
| Panjang (mm) 78 81 78 79 80 78 79 80 |
Rata-rata hasil pengukuran ini adalah 79,125 mm, dibulatkan menjadi 79 mm. Selisih terbesar antara nilai rata-rata dengan masing-masing pengukuran individual adalah 81 – 79,125 = 1,875 mm, dibulatkan menjadi 2 mm. Hasil pengukuran akhimya dinyatakan sebagai 79 ± 2 mm. Dengan demikian, kita nyatakan bahwa panjang yang sebenamya dari objek yang kita ukur berada di antara 77 mm sampai 81 mm.
Para ilmuwan telah menyepakati peijanjian sederhana mengenai kesalahan dalam pengukuran, yaitu jika kesalahan hasil pengukuran tidak disebutkan secara ekplisit, maka kesalahan pada suatu angka hasil pengukuran sama dengan setengah skala terkecil. Misalnya, 25 mm memiliki kesalahan 0,5 mm 25,00 mm memiliki kesalahan 0,005 mm
Dalam matematika, 25 mm = 25,00 mm, tetapi dalam fisika berlaku bahwa, 25 mm 4 25,00 mm, karena kedua angka ini memiliki besar kesalahan atau ketidak-pastian yang berbeda.
Perhitungan Yang Melibatkan Kesalahan Hasil Pengukuran
Secara umum, perhitungan angka-angka hasil pengukuran menambah besamya kesalahan atau ketidakpastian. Misalnya,
(12 ± 2) + (15 ± 3)
menghasilkan penjumlahan terkecil 10 + 12 = 22 dan penjumlahan terbesar 14 + 18 = 32 sehingga hasilnya kita tulis sebagai 27 ± 5. Terlihat bahwa penjumlahan tersebut memperbesar kesalahan hasil pengukuran.
Besarnya kesalahan semakin bertambah besar ketika kita mengalikan dua angka hasil pengukuran. Misalnya,
(12 ± 2) x (15 ± 3)
menghasilkan perkalian terkecil 10×12 = 120 dan perkalian terbesar 14 x 18 = 252. Hasil perkalian kita tulis sebagai 180 ± 66.
Jelas bahwa perhitungan yang melibatkan kesalahan hasil pengukuran semacam ini akan memakan cukup banyak waktu. Oleh karena itu, para ilmuwan menyepakati perhitungan angka-angka hasil pengukuran yang melibatkan kesalahan sebagai berikut.
- Ketika angka-angka dijumlahkan atau dikurangkan, maka kesalahan mutlaknya (atau kesalahan absolut) dijumlahkan. Misalnya, (15 ± 4) + (19 ± 5) = (34 ±9).
- Ketika angka-angka dikalikan atau dibagi, maka persen kesalahannya dijumlahkan. Misalnya, (20 ± 1) x (100 ± 10) = (20 ± 5%) x (100 ± 10%) = (20 x 100) ± (5% + 10%) = 2000 ± 15% = 2000 ± 300.
Demikian penjelasan yang bisa kami sampaikan tentang 6 Bentuk Kesalahan Dalam Pengukuran Dan Cara Penanganan Terlengkap. Semoga postingan ini bermanfaat bagi pembaca dan bisa dijadikan sumber literatur untuk mengerjakan tugas. Sampai jumpa pada postingan selanjutnya.
Baca postingan selanjutnya:
- Pengertian Dan Aturan Penulisan Angka Penting Dalam Fisika
- Cara Pengukuran Dengan Jangka Sorong Dan MIkrometer Sekrup
- Jenis Perkalian Vektor Fisika Lengkap Dengan Contohnya
- Cara Menentukan Vektor V Dalam Vektor Satuan Fisika
- Metode Penjumlahan Vektor Yang Tidak Tegak Lurus
- Cara Cepat Menentukan Resultan Vektor Dengan Metode Phytagoras