Rumus Menghitung Luas Permukaan dan Volume Bola – Bola adalah bangun ruang? Apa itu bola? Apa rumus luas permukaan dan volume bola? Sebutkan ciri-ciri bola? Apa saja sifat bola?
Baca Juga : Macam-Macam Bangun Ruang
Agar lebih memahaminya, kali ini kita akan membahas tentang pengertian bola, sifat, ciri, rumus, contoh soal bola dan cara penyelesaianya secara lengkap.
Pengertian Bangun Ruang Bola
Dalam geometri, bola adalah bangun ruang tiga dimensi yang dibentuk oleh titik-titik yang berjarak sama terhadap suatu titik yang disebut titik pusat bola dan bola hanya memiliki 1 sisi.
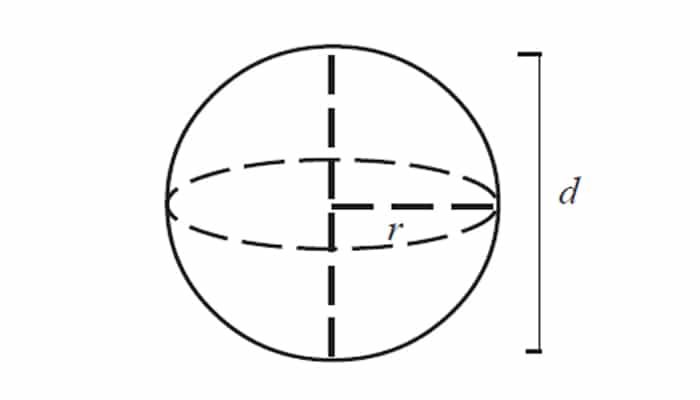
Dimensi bola dinyatakan dalam besaran jari-jari (r) atau diameter (d). Jari-jari atau radius bola adalah jarak antara permukaan bola dan titik pusat bola, sedangkan diameter bola adalah jarak garis lurus antara permukaan bola dengan permukaan sebrang titik pusat melalui titik pusat bola atau bisa dikatakan bahwa diameter bola sama dengan dua kali jari-jari bola.
Permukaan bola atau disebut juga kulit bola atau selimut bola adalah bidang yang membentuk permukaan bola. Luas permukaan bola atau disebutjuga luas kulit bola atau luas selimut bola.
Sifat-Sifat Bola
Berikut ini sifat atau ciri-ciri bola, diantaranya yaitu:
- Memiliki 1 buah bidang sisi.
- Memiliki 1 buah titik pusat.
- Memiliki 1 sisi lengkung tertutup.
- Tidak memiliki bidang datar.
- Tidak memiliki titik sudut dan rusuk.
- Memiliki jari jari yang tak terhingga dan semuanya sama panjang.
- Ruang garis yang menghubungkan dua titik pada bola disebut tali busur bola dan tali busur bola terpanjang disebut diameter bola.
Unsur-Unsur Bola
Berikut ini unsur-unsur dalam bangun ruang bola, diantaranya yaitu:
Jari-Jari
Jari-jari (r) adalah jarak dari titik pusat ke titik lain diluar bola.
Diameter
Diameter (d) adalah jarak antara dua titik terluar bola yang melewati titik pusat bola. Panjang diameter sama dengan 2x panjang jari-jari.
Sisi
Sisi adalah kumpulan titik yang berjarak sama dengan titik pusat.
Titik Pusat
Titik pusat bola adalah lokasi titik inti pada ukuran bola.
Baca Juga : Rumus Balok
Rumus Menghitung Luas Permukaan dan Volume Bola
Ada dua jenis bola dalam bangun ruang, yaitu bola pejal dan bola tidak pejal. Bola pejal adalah bola berbentuk padat atau keras sehingga tak berisi angin dan mempunyai kepadatan, contohnya bola bekel, buah jeruk, buah semangka dan lain sebagainya. Sedangkan, bola tidak pejal adalah bola yang didalamnya tidak memiliki kepadatan dan hanya berisi angin sehingga berongga, contohnya bola sepak, bola basker, bola voli dan lain sebagainya.
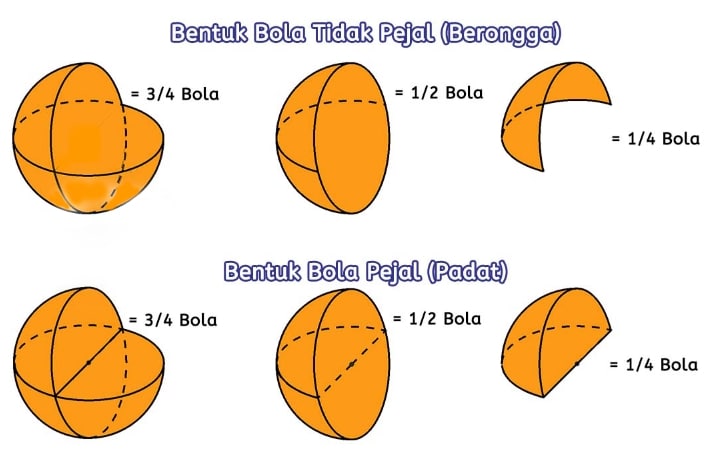
Rumus menghitung volume dan luas permukaan bola pejal dan tidak pejal ada persamaan pada bagian volume bola, ketidaksamaan pada bagian luas permukaan bola. Lebih jelasnya:
- Volume Bola Pejal Setengah = Volume Bola Tidak Pejal Setengah
- Volume Bola Pejal Seperempat = Volume Bola Tidak Pejal Seperempat
- Luas Permukaan Bola Pejal Setengah ≠ Luas Permukaan Bola Tidak Pejal Setengah
- Luas Permukaan Bola Pejal Seperempat ≠ Luas Permukaan Bola Tidak Pejal Seperempat
Rumus Luas Permukaan Bola
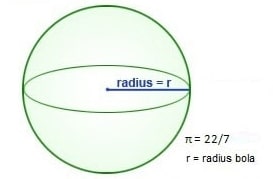
Luas permukaan bola = 4πr²
Rumus Luas Permukaan 3/4 Bola (Berongga)
Luas permukaan = 3/4 × Luas permukaan bola
Luas permukaan = 3/4 × 4 × π × r²
Luas permukaan = 3πr²
Baca Juga : Rumus Kubus
Rumus Luas Permukaan 3/4 Bola Pejal
Luas permukaan = 3/4 × Luas permukaan Bola + Luas alas Lingkaran Bola
Luas permukaan = 3/4 × 4 × π × r² + π × r²
Luas permukaan = 3 × π × r² + π × r²
Luas permukaan = 4πr²
Rumus Luas Permukaan 1/2 Bola (Berongga)
Luas permukaan = 1/2 × LP Bola
Luas permukaan = 1/2 × 4 × π × r²
Luas permukaan= 2πr²
Rumus Luas Permukaan 1/2 Bola Pejal
Luas permukaan = 1/2 × Luas permukaan Bola + Luas alas Lingkaran Bola
Luas permukaan = 1/2 × 4 × π × r² + π × r²
Luas permukaan = 2 × π × r² + π × r²
Luas permukaan = 3πr²
Rumus Luas Permukaan 1/4 Bola (Berongga)
Luas permukaan = 1/4 × Luas permukaan Bola
Luas permukaan = 1/4 × 4 × π × r²
Luas permukaan = πr²
Rumus Luas Permukaan 1/4 Bola Pejal
Luas permukaan = 1/4 × Luas permukaan Bola + Luas alas Lingkaran Bola
Luas permukaan = 1/4 × 4 × π × r² + π × r²
Luas permukaan = π × r² + π × r²
Luas permukaan = 2πr²
Rumus Volume Bola
Volume = 4/3 x π × r³
Rumus Volume Seperempat Bola dan Bola Pejal Tiga Seperempat
V = 3/4 × 4/3 × π × r³
V = πr³
Rumus Volume Setengah Bola dan Bola Pejal Setengah
V = 1/2 × 4/3 × π × r³
V = 2/3 × π × r³
Rumus Volume Seperempat Bola dan Bola Pejal Seperempat
V = 1/4 × 4/3 × π × r³
V = 1/3 × π × r³
Rumus Jari-Jari Bola
Jika Diketahui Diameter Bola
r = d ÷ 2
Jika Diketahui Luas Permukaan Bola

Jika Diketahui Volume Bola
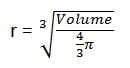
Rumus Diameter Bola
Jika Diketahui Jari-Jari Bola
d = r × 2
Jika Diketahui Volume Bola
r = ³√((3×V)/(4×π)) × 2
atau
r = ³√((V/π) × 3/4) × 2
Jika Diketahui Luas Permukaan Bola
r = √(luas permukaan /(4 × π)) × 2
Baca Juga : Rumus Tabung
Contoh Soal Menghitung Luas Permukaan dan Volume Bola
Berikut ini contoh soal bola dan pembahasannya:
1. Diketahui jari-jari sebuah bola sepak yaitu 7 cm, jika π = 22/7 maka berapakah volume bola tersebut?
Pembahasan:
Diketahui:
r= 7 cm
π = 22/7
Ditanya: Volume bola?
Jawab:
V = 4/3 π x r³
V = 4/3 x 22/7 x 7³
V = 4/3 x 22/7 x 343
V = 1437.3 cm³
2. Sebuah bola berdiameter 24 cm. Berapakah volume bola tersebut?
Pembahasan:
Diketahui :
d = 24 cm
r = 1/2. d
r = 1/2. 24
r = 12 cm
Ditanya : Volume bola?
Jawab :
v = 4/3 π x r³
V = 4/3 x 22/7 x 12³
V = 4/3 x 22/7 x 1728
V = 7234,56 cm³
3. Diketahui sebuah bola memiliki jari-jari sebesar 20 cm, tentukan luas permukaan bola!
Pembahasan:
Diketahui:
r = 20 cm
Ditanya: Luas permukaan?
Jawab:
L = 4πr²
L = 4 x 3,14 x 20cm x 20cm
L = 5.024 cm²
Baca Juga : Rumus Kerucut
5. Terdapat 2 buah bola dengan jari-jari secara berurutan 10 cm dan 20 cm. Tentukan perbandingan volume dan perbandingan luas permukaan kedua bola tersebut!
Pembahasan:
Perbandingan volume kedua bola tersebut sama dengan perbandingan pangkat 3 dari jari-jari bola:
V1 : V2 = r1³ : r2³
V1 : V2 = 10³ : 20³
V1 : V2 = 1000 : 8000
V1 : V2 = 1 : 8
Perbandingan luas permukaan kedua bola tersebut sama dengan perbandingan kuadrat jari-jari bola:
L1 : L2 = r1² : r2²
L1 : L2 = 10²: 20²
L1 : L2 = 100 : 400
L1 : L2 = 1 : 4
6. Sebuah bola dipotong menjadi 2 dengan jari-jari 60 cm, berapakah besar volume bola tersebut?
Pembahasan:
Diketahui:
r = 60 cm
Ditanya: volume?
Jawab:
v = 1/2 x 4/3 x π x r³
v = 2/3 x 3,14 x 60 cm x 60 cm x 60 cm
v = 45216 cm³
7. Sebuah bola basket memiliki diameter 24 cm. Berapakah volume udara didalam bola basket tersebut?
Pembahasan:
Diketahui:
d = 24 cm, maka r = 12 cm
Ditanya: volume udara dalam bola?
Jawab:
V = 4/3πr³
V = 4/3 x 3,14 x 12 cm x 12 cm x 12 cm
V = 7234,56 cm³ atau 7,23456 liter
8. Sebuah pabrik akan memproduksi 20.000 buah bola dengan diameter bolanya 20 cm. Berapa luas bahan plastik yang yang dibutuhkan untuk membuat bola tersebut?
Pembahasan:
Diketahui:
d = 20 cm
r = 10 cm
Bola yang ingin di produksi = 20.000 buah
Baca Juga : Macam-Macam Bangun Datar
Ditanya: luas bahas plastik untuk membuat bola?
Jawab:
Luas 20.000 bola = 20.000 x 4 x π x r²
Luas 20.000 bola = 20.000 x 4 x 3,14 x 10²
Luas 20.000 bola = 25.120.000 cm²
Luas 20.000 bola = 2512 m²
9. Sebuah bola memiliki diameter sebesar 14 cm. Berapakah volume bola tersebut!
Pembahasan:
Diketahui:
d = 14 cm
Ditanya: volume?
Jawab:
Pertama, hitung jari-jari:
r = d ÷ 2
r = 14 ÷ 2
r = 7 cm
V = 4/3 × π × r³
V = 4/3 × 22/7 × 7³
V = 4/3 × 1078
V = 1437,33 cm³
10. Berapakah luas permukaan bola dengan diameter 28cm!
Pembahasan:
Diketahui:
d = 28 cm
Ditanya: luas permukaan?
r = d ÷ 2
r = 28 ÷ 2
r = 14 cm
Luas permukaan = 4 × π × r²
Luas permukaan = 4 × 22/7 × 14²
Luas permukaan = 4 x 2156
Luas permukaan = 8624 cm²
11. Sebuah semangka berbentuk bola dibelah menjadi 4 bagian sama rata, jika buah semangka tersebut memiliki jari-jari 14 cm. Berapakah volume pada setiap semangka?
Pembahasan:
Diketahui:
1 semangka dibagi 4 = 1/4 bagian
Jari-jari = 14 cm
Ditanya: volume 1/4 semangka?
Jawab:
V = 1/4 × 4/3 × π × r³
V = 1/3 × π × r³
V = 1/3 × 22/7 × 14³
V = 1437,33 cm³
12. Sebuah bola karet mempunyai luas permukaan 2464 cm². Hitunglah jari-jari bola karet tersebut?
Pembahasan:
Dikatahui:
Luas permukaan = 2464 cm²
Ditanya: jari-jari?
Jawab:
r = √(luas permukaan/(4 × π))
r = √(2464 / (4 × 22/7))
r = √(2464/12,57)
r = √196,02
r = 14 cm
Baca Juga : Rumus Segitiga
Demikian artikel pembahasan tentang pengertian bola, sifat, ciri, rumus, contoh soal bola dan cara penyelesaianya secara lengkap. Semoga bermanfaat
Read more. cialis price in south africa Read This Next.