Rumus Menghitung Luas Permukaan dan Volume Balok – Balok adalah bangun? Apa yang dimaksud balok? Apa itu balok? Apa rumus luas permukaan dan volume balok? Sebutkan unsur-unsur balok! Apa saja ciri-ciri balok? Berikan contoh jaring-jaring balok!
Baca Juga : Macam-Macam Bangun Ruang
Agar lebih memahaminya, kali ini kita akan membahas tentang pengertian balok, sifat, unsur, jaring-jaring balok, rumus, contoh soal balok dan cara penyelesaiannya secara lengkap.
Pengertian Balok
Balok adalah bangun ruang tiga dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang dengan setidaknya memiliki sepasang sisi sejajar berukuran berbeda. Balok memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Balok yang dibentuk oleh enam persegi sama dan sebangun disebut dengan bangun kubus.
Contoh bangun balok dalam kehidupan sehari-hari diantaranya lemari, kotak pensil, kulkas dan lain sebagainya.
Sifat-Sifat Balok
Berikut ini sifat atau ciri-ciri balok, diantaranya:
- Memiliki 6 sisi, 12 rusuk dan 8 titik sudut.
- Sisi-sisi balok berbentuk persegi panjang.
- Rusuk-rusuk yang sejajar memiliki ukuran sama panjang.
- Setiap diagonal bidang pada sisi yang berhadapan memiliki ukuran sama panjang.
- Setiap diagonal ruang pada balok memiliki ukuran sama panjang.
- Setiap bidang diagonal pada balok memiliki bentuk persegi panjang.
Unsur-Unsur balok
Berikut ini unsur-unsur pada bangun balok, diantaranya:
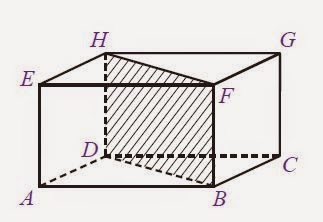
Sisi atau Bidang
Sisi balok adalah bidang yang membatasi balok. Balok memiliki 6 sisi. Perhatikan gambar diatas yang merupakan yang merupakan sisi adalah sisi bawah (ABCD); sisi atas (EFGH); sisi depan (ABFE); sisi belakang (DCGH);sisi samping kiri (BCGF); dan sisi samping kanan(ADHE).
Balok memiliki 3 pasang sisi yang sama bentuk dan ukurannya. Pasangan tersebut adalah:
- Sisi ABFE = sisi DCGH
- Sisi ABCD = sisi EFGH
- Sisi BCGF = sisi ADHE.
Rusuk
Rusuk adalah garis potongan antar dua sisi bidang balok dan terlihat seperti kerangka yang menyusun balok. Sama seperti kubus, balok memiliki 12 rusuk . Perhatikan gambar kubus diatas yang merupakan rusuk adalah AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, dan HD.
Titik Sudut
Titik Sudut adalah titik potongan antara dua atau 3 rusuk. Balok memiliki 8 titik sudut. Perhatikan gambar diatas, yang merupakan titik sudut yaitu A, B, C, D, E, F, G, dan H.
Baca Juga : Rumus Kubus
Diagonal Bidang atau Diagonal Sisi
Diagonal bidang atau diagonal sisi adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan pada setiap bidang atau sisi balok. Sama halnya dengan kubus, balok memiliki 12 Diagonal bidang. Perhatikan gambar diatas, yang merupakan diagonal bidang yaitu AF, BE, BG, CF, CH, DG, DE, AH, AC, BD, EG, dan HF.
Diagonal Ruang
Diagonal ruang adalah garis yang menghubungkan 2 titik sudut yang saling berhadapkan dalam satu ruang. Sama halnya dengan kubus, balok memiliki 4 diagonal ruang. Perhatikan gambar diatas, yang merupakan diagonal ruang yaitu AG , BH, CE dan DF.
Bidang Diagonal
Bidang diagonal adalah bidang yang dibatasi oleh dua rusuk dan dua diagonal bidang. Sama halnya dengan kubus, balok memiliki 6 bidang diagonal. Perhatikan gambar diatas, yang merupakan bidang diagonal yaitu ACGE, AFGD, CDEF, BFHD, dan BEHC.
Selain itu, balok memiliki beberapa elemen diantaranya:
- Panjang(p) yaitu rusuk yang terpanjang dari alas balok.
- Lebar (l) yaitu rusuk terpendek dari sisi alas balok.
- Tinggi (t) yaitu rusuk yang tegak lurus terhadap panjang dan lebar balok.
Jaring-Jaring Balok
Jaring-jaring adalah bidang datar yang berupa gabungan dari bangun datar yang membentuk sebuah bangun ruang seperti balok, kubus, limas dan lain sebagainya. Jaring-jaring bisa diperoleh dari membagi sebuah bangun ruang dengan mengikuti rusuk-rusuknya.
Jaring-jaring balok terdiri dari 6 buah bangun datar persegi atau persegi panjang. Berikut ini gambar cara membuat jaring-jaring balok:
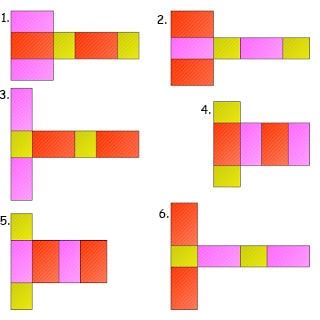
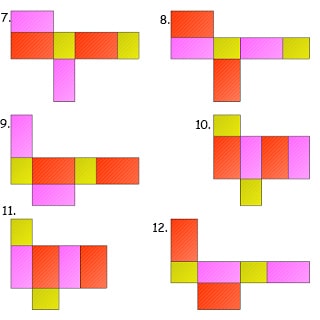
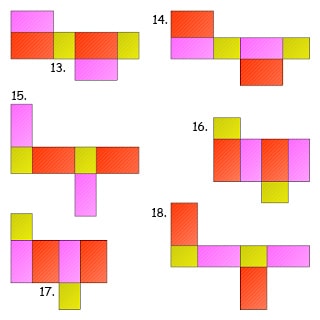
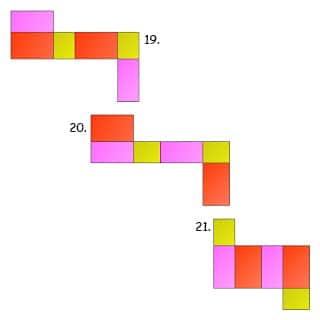
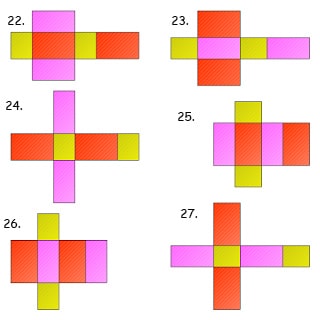
Baca Juga : Rumus Tabung
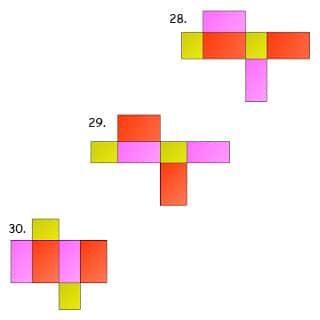
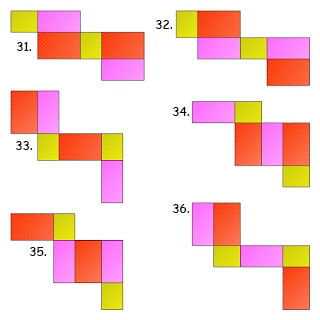
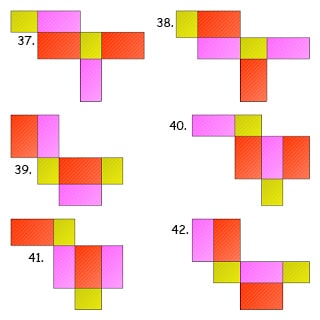
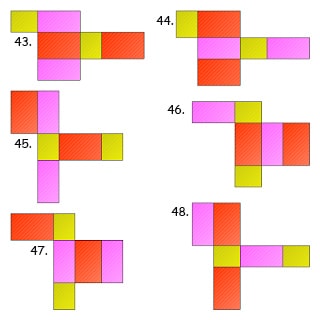
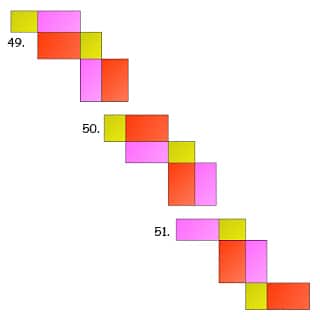
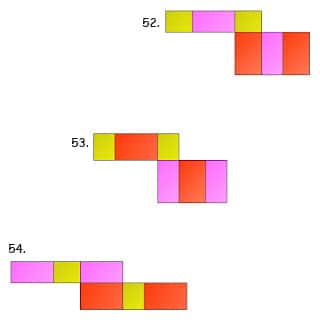
Rumus Balok
Luas Permukaan
L : 2.(p.l+p.t+l.t)
Volume
V : p.l.t
Panjang Diagonal Ruang
Dr : √(p2+l2+t2)
Panjang Diagonal Bidang
Db1 : √(s2+s2)
Db2 : √(s2+s2)
Db3 : √(s2+s2)
Luas Bidang Diagonal
Lb1 : Db1.t
Lb2 : Db2.l
Lb3 : Db3.p
Baca Juga : Rumus Kerucut
Contoh Soal Balok
Berikut ini contoh soal balok dan pembahasannya:
1. Diketahui sebuah balok berukuran sebagai berikut!
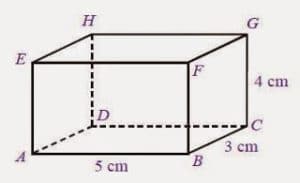
a. Tentukan luas permukaan balok!
b. Tentukan Volume balok!
Pembahasan:
Diketahui:
p = 5 cm
l = 3 cm
t = 4 cm
Ditanya:
a. Luas permukaan (L)?
b. Volume (V)?
Jawab:
A. Luas Permukaan Balok
L : 2.(p.l+p.t+l.t)
L : 2.(5.3+5.4+3.4)
L : 2.(15+20+12)
L : 2 (47)
L : 94
Jadi luas permukaan balok adalah 94 cm2.
B. Volume Balok
V : p.l.t
V : 5.3.4
V : 60
Jadi Volume balok tersebut adalah 60 cm3.
2. Perhatikan gambar balok dibawah ini!
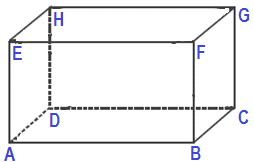
Diketahui panjang AB= 12 cm, BC = 8 cm dan AE = 5 cm. Hitunglah:
a. Panjang AF
b. Panjang AC
c. Panjang AH
Pembahasan:
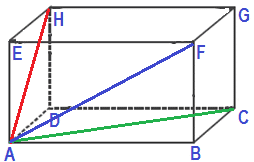
a). Panjang AF dapat dihitung dengan teorema phytagoras. Perhatikan segitiga ABF siku-siku di B, maka:
AF = √(AB2 + BF2)
AF = √(122 + 52)
AF = √(144 + 25)
AF = √169
AF = 13 cm
b). Perhatikan segitiga ABC siku-siku di B, maka:
AC = √(AB2 + BC2)
AF = √(122 + 82)
AF = √(144 + 64)
AF = √208
AF = 4√13 cm
Baca Juga : Macam-Macam Bangun Datar
c). Perhatikan segitiga AEH siku-siku di E, maka:
AC = √(AE2 + EH2)
AF = √(52 + 82)
AF = √(25 + 64)
AF = √89 cm
3. Sebuah balok memiliki panjang 12 cm, lebar 8 cm dan tinggi 4 cm. Hitunglah berapa panjang diagonal ruang balok?
Pembahasan:
Diketahui:
p = 12 cm
l = 8 cm
t = 4 cm
Ditanya: Diagonal ruang (Dr)?
Jawab:
Dr : √(p2+l2+t2)
Dr : √(122+82+42)
Dr : √244
Dr : 4√14
4. Perhatikan gambar balok di bawah berikut ini!
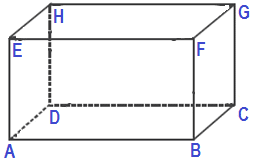
Diketahui panjang AB = 12 cm, BC = 8 cm dan AE = 6 cm. Hitunglah luas bidang diagonal ABGH!
Pembahasan:
Jika digambarkan akan tampak seperti gambar di bawah ini.
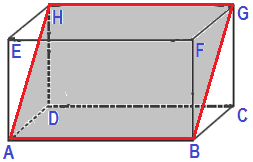
Terlebih dahulu harus cari panjang BG dengan teorema phytagoras.
BG = √(BC2 + CG2)
BG = √(82 + 62)
BG = √(64 + 36)
BG = √100
BG = 10 cm
Luas bidang diagonal ABGH dapat dicari dengan rumus persegi panjang, yaitu:
Luas ABGH = AB . BG
Luas ABGH = 12 cm . 10 cm
Luas ABGH = 120 cm2
5. Perhatikan gambar berikut!
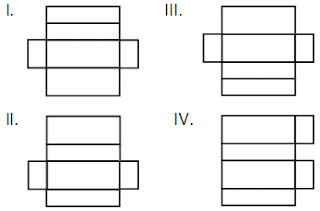
Yang merupakan jaring-jaring adalah. . . .
A. I
B. II
C. III
D. IV
Jawaban : B. II
Baca Juga : Rumus Segitiga
6. Gambar berikut yang merupakan jaring-jaring balok adalah……….
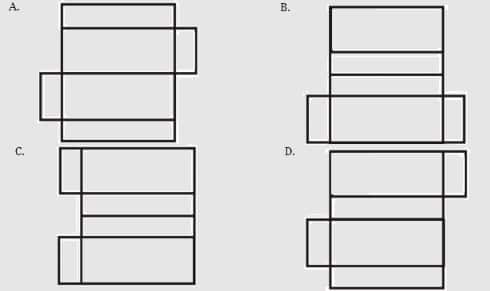
Jawaban : d
7. Gambar berikut yang bukan merupakan jaring-jaring balok adalah……
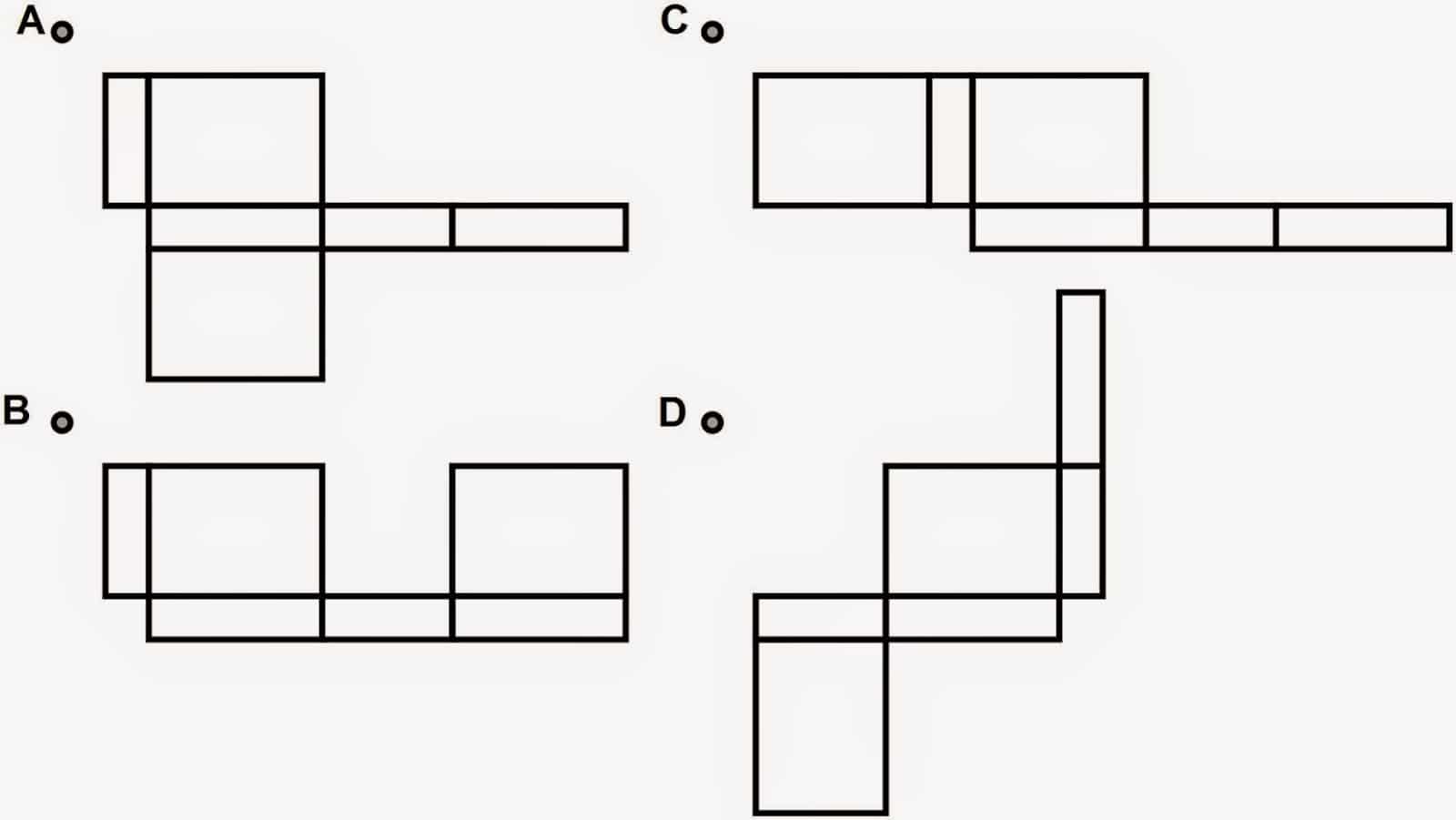
Jawaban : b
8. Perhatikan gambar berikut!
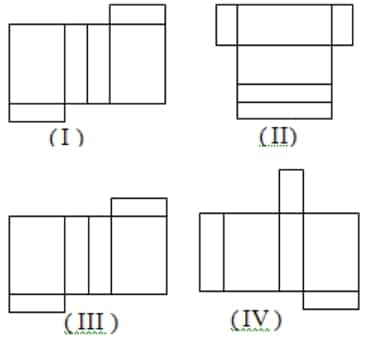
Yang merupakan jaring-jaring balok adalah nomor………
A. I dan II
B. I dan IV *
C. II dan III
D. II dan IV
Jawaban: B. I dan IV
9. Tentukan bentuk bangun datar dari jaring jaring balok, jika diketahui Balok ABCD.EFGH dipotong pada rusuk tertentu.
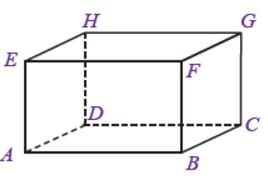
Pembahasan:
Bentuk datar yang dihasilkan yaitu:
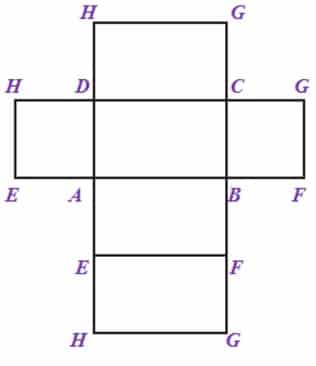
Baca Juga : Rumus Persegi Panjang
Penjelasan :
Jaring-jaring balok berupa 6 buah persegi panjang yang terdiri dari 3 pasang persegi panjang yang sama besar. Berdasarkan gambar tersebut diperoleh bahwa pada balokk ABCD.EFGH, terdapat:
- Persegi panjang ABCD sama dengan EFGH.
- Persegi panjang EHDA sama dengan BCGF.
- Persegi panjang ABFE sama dengan DCGH.
10. Sebuah kardus berbentuk balok volumenya 160 cm3. Jika panjang kardus 8 cm dan tinggi kardus 5 cm, tentukan lebar kardus tersebut.
Pembahasan:
Diketahui:
V = 160 cm3
p = 8 cm
t = 5 cm
Ditanya: lebar?
Jawab:
V = p.l.t
160 cm3 = 8 cm.l. 5 cm
l = 160 cm3/40 cm
l = 4 cm
11. Volume sebuah balok 90 cm3. Jika panjang balok 6 cm dan lebar balok 5 cm, tentukan tinggi balok tersebut.
Pembahasan:
Diketahui:
V = 90 cm3
p = 6 cm
l = 5 cm
Ditanya: tinggi?
Jawab:
Vbalok = p.l.t
90 cm3 = 6 cm x 5 cm x t
90 cm3 = 30 cm2 x t
t = 90 cm3/30 cm2
t = 3 cm
13. Sebuah balok memiliki panjang 12cm, lebar 10 cm dan tinggi 5 cm, hitunglah volume balok tersebut!
Pembahasan:
Diketahui:
p = 12 cm
l = 10 cm
t = 5 cm
Ditanya: volume?
Jawab :
V = p x l x t
V = 12 cm x 10 cm x 5 cm
V = 600 cm3
13. Pak Indra memiliki kolam berbentuk balok dengan tinggi 40 cm, lebar 60 cm dan panjang 80cm. Bak tersebut akan diisi air. Berapa banyak air yang dibutuhkan untuk mengisi 3/4 bagian kolam tersebut!
Pembahasan:
Diketahui:
p = 80 cm
l = 60 cm
t = 40 cm
Ditanya: 3/4 volume balok (v)
Jawab:
3/4 x V = p x l x t
V = 3/4 (80 cm x 60 cm x 40 cm)
V = 3/4 (192.000 cm3 )
V = 144.000 cm3
Baca Juga : Rumus Belah Ketupat
14. Sebuah kolam sampah memiliki lebar 40 cm, dengan panjang 3/2 kali lebarnya dan tinggi kolam sampah 5 lebihnya dari ukuran lebar. Berapakah volume kolam sampah tersebut?
Pembahasan:
Diketahui:
l = 40 cm
p = 3/2 x (l) = 3/2 x 40 = 60 cm
t = l + 5 = 40 cm + 5 cm = 45 cm
Ditanya: volume?
Jawab:
V = p x l x t
V = 60 cm x 40 cm x 45 cm
V = 108.000 cm3
15. Suatu tempat beras berbentuk balok dengan panjang 10 cm, lebar 25 cm, dan tinggi 1m. kawasan beras tersebut akan diisi penuh dengan beras seharga Rp. 9.000,00 perliter. Berapa banyak uang yang dibutuhkan untuk membeli beras tersebut?
Pembahasan:
Diketahui :
p = 10 cm,
l = 25cm,
t= 1 m = 100 cm
Harga 1 liter beras = Rp.9000,00
Ditanya: jumlah uang yang dibutuhkan untuk membeli beras?
Jawab:
Volume tempat beras = p x l x t
V = p x l x t
V = 10 cm x 25 cm x 100 cm
V = 25.000 cm3
V = 25 liter
maka, harga 25 liter beras = 25 x Rp. 9.000,- = Rp.225.000,00
Demikian artikel pembahasan tentang pengertian balok, sifat, unsur, jaring-jaring balok, rumus, contoh soal balok dan cara penyelesaiannya secara lengkap. Semoga bermanfaat
It is also not reimbursed by social security. cialis price However, it is priced differently in a pharmacy and online.