Rumus Luas dan Keliling Lingkaran – Apa pengertian lingkaran dalam matematika? Lingkaran Apa yang dimaksud dengan lingkaran? Apa saja unsur unsur lingkaran? Apa rumus menghitung keliling dan rumus lingkaran?
Baca Juga : Macam-Macam Bangun Datar
Agar lebih memahaminya, kali ini kita akan membahas tentang pengertian lingkaran, sifat, unsur, rumus, contoh soal lingkaran dan pembahasannya secara lengkap.
Pengertian Lingkaran
Lingkaran adalah himpunan semua titik pada bidang dalam jarak tertentu yang disebut dengan jari-jari dari seatu titik yang disebut dengan pusat.
Sifat-Sifat Lingkaran
Sifat atau ciri-ciri lingkaran, diantaranya yaitu:
- Mempunyai simetri putar tak terhingga.
- Mempunyai simetri lipat serta sumbu yang tak terhingga.
- Tidak memiliki titik sudut.
- Memiliki satu sisi.
Unsur-Unsur Lingkaran
Berikut ini unsur atau bagian lingkaran:
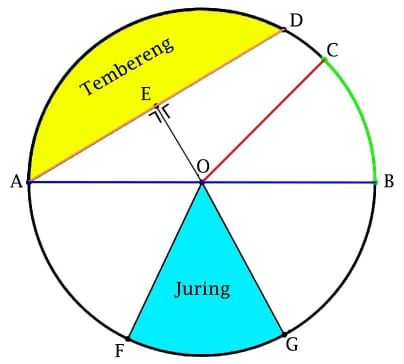
Keterangan:
O = titk pusat
AB = diameter
OC = jari-jari (r)
AD = tali busur
BC = busur
OE = apotema
Titik Pusat
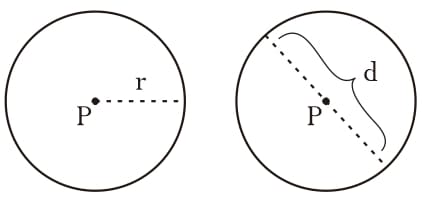
Titik pusat (P) adalah titik tengah lingkaran, dimana jarak titik tersebut dengan titik manapun pada lingkaran selalu tetap.
Jari-Jari
Jari-jari (R) adalah garis lurus yang menghubungkan titik pusat dengan lingkaran.
Tali Busur
Tali busur (TB) adalah garis lurus dalam lingkaran yang memotong lingkaran pada dua titik yang berbeda.
Busur
Busur (B) adalah garis lengkung baik terbuka, maupun tertutup yang berimpit dengan lingkaran.
Keliling Lingkaran
Keliling lingkaran (K) adalah busur terpanjang pada lingkaran.
Diameter
Diameter (D) adalah tali busur terbesar yang panjangnya adalah dua kali dari jari-jarinya. Diameter membagi lingkaran sama luas.
Apotema
Apotema adalah garis terpendek antara tali busur dan pusat lingkaran.
Juring
Juring (J) adalah daerah pada lingkaran yang dibatasi oleh busur dan dua buah jari-jari yang berada pada kedua ujungnya.
Baca Juga : Rumus Layang-Layang
Tembereng
Tembereng (T) adalah daerah pada lingkaran yang dibatasi oleh sebuah busur dengan tali busurnya.
Cakram
Cakram (C) adalah semua daerah yang berada di dalam lingkaran. Luas cakram yaitu jari-jari kuadrat dikali pi. Cakram merupakan juring terbesar.
Sudut Pusat dan Sudut Keliling
Sudut pusat adalah sudut dengan derajat tertentu yang dibentuk oleh dua buah jari-jari yang menghadap pada sebuah busur lingkaran. Sedangkan, sudut keliling adalah sebuah sudut pada lingkaran yang dibentuk oleh dua buah tali busur. Perbedaan sudut pusat dan sudut keliling terdapat pada elemen pembentuknya, sudut pusat dibentuk oleh dua buah jari-jari sedangkan sudut keliling dibentuk oleh dua buah tali busur.
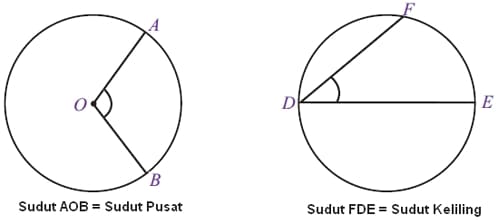
Sudut pusat dan sudut lingkaran yang memenuhi kriteria tertentu bisa memiliki hubungan.
“Jika terdapat sudut pusat lingkaran dan sudut keliling lingkaran yang menghadap pada tali busur lingkaran yang sama maka dua kali sudut lingkaran sama dengan nilai sudut pusat.”
- Sudut Pusat = 2 x Sudut Keliling
- Sudut Keliling = 1/2 x sudut pusat
Sifat sudut pusat dan sudut keliling lingkaran, diantaranya yaitu:
1. Sudut keliling yang menghadap diameter lingkaran selalu membentuk sudut 90 derajat atau biasa disebut dengan sudut siku-siku.
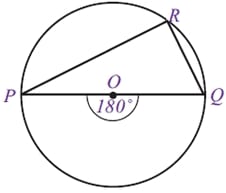
Sudut PRQ besarnya adalah 90 derajat.
2. Sudut keliling yang menghadap busur yang sama akan memiliki besar sudut yang sama pula.
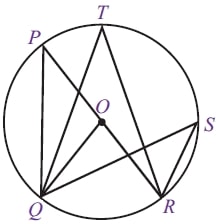
Menurut sifat di atas maka besarnya ∠QPR = ∠QTR = ∠QSR
3. Sudut-sudut keliling yang saling berhadapan akan memiliki jumlah total sudut 180 derajat.
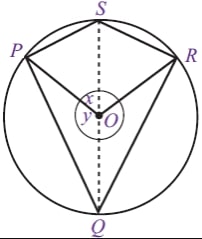
∠PSR + ∠PQR = 180 derajat
Sudut Diantara Dua Tali Busur
Soal yang melibatkan dua tali busur yang saling berpotongan sering kali cukup membingungkan. Jika perpotongan tepat pada garis lingkaran akan sangat mudah. Namun jika perpotongannya terjadi di dalam sebuah lingkaran atau di luar lingkaran akan cukup membingungkan.
a. Saling Berpotongan Di Dalam Lingkaran
Jika terdapat dua tali busur yang saling berpotongan di dalam sebuah lingkaran maka besar sudut antara dua tali busur yang berpotongan di dalam sebuah lingkaran tersebut sama dengan setengah kali dari jumlah sudut pusat yang tepat berada di depan dan dibelakannya. Perhatikan contoh berikut ini.
Baca Juga : Rumus Trapesium
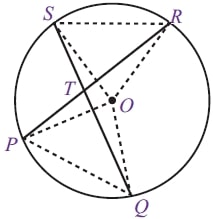
∠PTS = ½ (∠POS + ∠QOR)
∠STR = ½ (∠SOR + ∠POQ)
b. Saling Berpotongan Di Luar Lingkaran
Jika terdapat dua tali busur saling berpotongan di luar lingakaran maka besar sudut antara dua tali busur yang berpotongan di luar lingkaran ialah setengah kali selisih sudut pusat yang terletak diantara kedua tali busur tersebut.
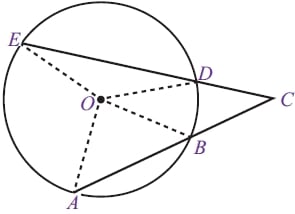
∠TRP = ½ (∠TOP – ∠SOP)
Rumus Lingkaran
Luas Lingkaran
L = π x r x r
L = π x r²
Keliling Lingkaran
K = π x d
K = 2πr
K = π x 2 x r
Diameter Lingkaran
d = 2 × r
Jari-jari Lingkaran
r = d : 2
Mencari r Lingkaran
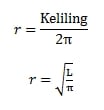
Cara Mencari Panjang Busur, Tali Busur, Luas Juring dan Tembereng Lingkaran
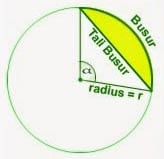
Rumus Panjang Busur
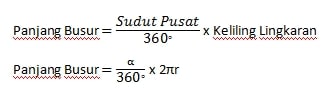
Rumus Panjang Tali Busur
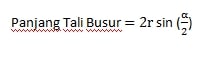
Rumus Luas Juring
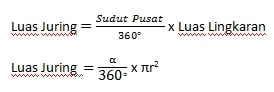
Baca Juga : Rumus Jajar Genjang
Rumus Segitiga
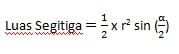
Rumus Luas Tembereng
Luas Tembereng = Luas Juring – Luas Segitiga
![]()
Keterangan:
π = 3,14 atauu 22/7
π = 22/7 digunakan jika jari-jari (r) atau diameter (d) merupakan kelipatan 7 atau bisa dibagi 7
π = 3,14 digunakan jika jari-jari (r) atau diameter (d) bukan kelipatan 7 atau tidak bisa dibagi 7
r = jari-jari
d = diameter (2 x r)
α = sudut pusat, sudut yang menghadap ke tali busur.
Contoh Soal Lingkaran
Berikut ini contoh soal lingkaran dan cara penyelesaiannya:
1. Roda berbentuk lingkaran memiliki diameter sebesar 30 cm. Tentukan luas lingkaran dan keliling lingkaran tersebut!
Pembahasan:
Diketahui:
d = 30 cm, maka r = 30/2 = 15
Ditanya: Luas dan Keliling?
Jawab:
a. Luas
Luas = π.r²
Luas = 3,14 x 15²
Luas = 3,14 x 225 = 707 cm²
b. Keliling
Keliling = 2.π.r
K = 2. 22/7.15
K = 30 x 22/7
K = 660/7
K = 95 cm
2. Perhatikan gambar dibawah ini!
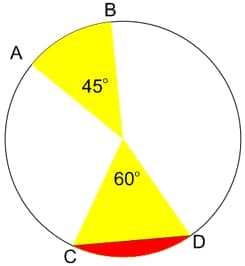
Jika diketahui panjang busur AB = 33 cm dan luas juring COD = 924 cm², maka tentukanlah:
a. Panjang Busur CD
b. Luar Juring AOB
c. Luas Tembereng CD.
Pembahasan:
a. Panjang Busur AB/CD = ∠ AOB/∠ COD
Panjang Busur CD = ∠COD/∠AOB x Panjang Busur AB
Panjang Busur CD = 60/45 x 33 = 44 cm
b. Luas Juring AOB/COD = ∠ AOB/∠ COD
Luas Juring AOB = ∠ AOB/∠ COD x Luas Juring COD
Luas Juring AOB = 45/60 x 924 = 693 cm²
c. Luas Tembereng CD
Jika kalian perhatikan lagi tentang lingkaran di atas, maka dengan sudut 60º maka panjang OC = OD = CD = jari-jari lingkaran. Untuk mencari jari-jari lingkarannya kalian bisa menggunakan perbandingan sudut untuk mencari keliling lingkaran baru kemudian kalian cari panjang jari-jari nya.
Panjang Busur CD/Keliling lingkaran = 60/360
Keliling lingkaran = Panjang Busur CD x 360/60
Keliling lingkaran = 44 x 6
2πr = 44 x 6
πr = 132
22/7 x r = 132
r = 132/22 x 7 = 42.
Baca Juga : Rumus Segitiga
Setelah kalian menemukan r selanjutnya bisa menetukan tinggi segitiga ODC dengan menggunakan dalil phytagoras atau rumus segitiga sama sisi. Kita coba dengan dalil phytagoras
t = √(422-212)
t = √(1,764-441
t = √1.323
t = 21√3
Luas Segitiga ΔOCD = 0,5 x 42 x 21√3
Luas Segitiga ΔOCD = 441√3
Luas Tembereng CD
Luas Tembereng CD = Luas Juring COD – Luas ΔOCD
Luas Tembereng CD = 924 – 441√3 cm²
Luas Tembereng CD = 483√3 cm²
3. Sebuah lingkaran memiliki jari-jari 8 cm. Berapakah keliling lingkaran tersebut?
Pembahasan:
Diketahui:
r = 8 cm
π = 3,14 atauu 22/7
Ditanya: Keliling?
Jawab:
K = 2πr
K = 2.3,14.8
K = 50,24 cm
4. Sebuah kolam ikan berbentuk lingkaran dengan diameter 12 m, berapakah keliling dari kolam ikan tersebut?
Pembahasan:
Diketahui:
d = 12 m
Ditanya: keliling?
Jawab:
K = π x d
K = 3,14 x 12 = 37,68 m
5. Sebuah kertas dipotong membentuk lingkaran memiliki jari-jari 14 cm, tentukan luas kertas tersebut!
Pembahasan:
Diketahui:
r = 14 cm
π = 3,14 atauu 22/7
Ditanya: luas?
Jawab:
L = π x r x r
L = 22/7 x 14 x 14
L = 616 cm²
6. Sebuah keliling lingkaran memiliki keliling 154 cm. Berapakah jari-jari lingkaran tersebut? (no 3)
Pembahasan:
Diketahui:
K = 154 cm
π = 3,14 atauu 22/7
Ditanya: r…?
Jawab:
K = π x d atau π x 2 x r
2r = K : π
2r = 154 : 22/7
2r = 154 x 7/22
2r = 49
r = 49/2
r = 24,5 cm
7. Sebuah kertas berbentuk lingkaran dengan keliling 616 cm. Tentukan diameter kertas tersebut!
Pembahasan:
Diketahui:
K = 616 cm
π = 3,14 atauu 22/7
Ditanya: d…?
Jawab:
d = K : π
d = 616 : 22/7
d = 616 x 7/22
d = 196 cm
8. Dila memiliki hulahop dengan keliling 220 cm. Tentukan jari-jari hulahop tersebut!
Pembahasan:
Diketahui:
K = 220 cm
π = 3,14 atauu 22/7
Ditanya: r…?
Jawab:
K = π x d atau π x 2 x r
2r = K : π
2r = 220: 22/7
2r = 220 x 7/22
2r = 70
r = 70/2
r = 35 cm
9. Luas sebuah lingkaran adalah 2.464 cm². Tentukan keliling lingkaran tersebut!
Baca Juga : Rumus Persegi Panjang
Pembahasan:
Diketahui:
L = 2.464 cm²
π = 3,14 atauu 22/7
Ditanya: K…?
Jawab:
L = π x r²
r² = L : π
r² = 2.464 : 22/7
r² = 2.464 x 7/22
r² = 784
r = √784
r = 28
Jadi, d = 2r = 2.28 = 56 cm
K = π x d
K = 22/7 x 56
K = 176 cm
10. Sebuah taman berbentuk lingkaran dengan diameter 56 meter akan ditanami rumput. Harga rumput adalah RP 8.000,00/m². Berapa biaya yang harus dikeluarkan untuk membeli rumput tersebut?
Pembahasan:
Diketahui:
d = 56 m, jadi r = 28 m.
Harga rumput = RP 8.000,00/m²
Ditanya: biaya untuk membeli rumput?
Jawab:
Untuk memgetahui harga rumput, kita harus mengetahui luas lingkaran.
L = π x r²
L = 22/7 x 28 x 28
L = 2.464 m²
Maka,
Harga rumput = 2.464 m2 x RP 8.000,00/m²
Harga rumput = Rp 19.712.000,00
11. Sebuah kolam renang berbentuk lingkaran memiliki diameter 60 meter. Kolam tersebut dikelilingi jalan setapak selebar 1 meter. Berapa luas jalan setapak tersebut?
Pembahasan:
Diketahui:
d kolam = 60 m, maka r = 30 m
Lebar jalan = 1 m
Diameter kolam + lebar jalan = diameter lingkaran besar
Diameter lingkaran besar = 60 m + (2 x 1 m) = 62 m, jadi r = 31 m
Ditanya: luas jalan?
Jawab:
(L kolam + L jalan) = luas lingkaran besar
L lingkaran besar = π x r²
L lingkaran besar = 3,14 x 31 x 31
L lingkaran besar = 3017,54 m²
L kolam = 3,14 x 30 x 30
L kolam = 2826 m²
Luas jalan = (L kolam + L jalan) – L kolam
Luas jalan = 3017,54 m² – 2826 m² = 191,54 m²
Jadi luas jalan adalah 191,54 m²
12. Ibu membuat alas gelas berbentuk lingkaran berdiameter 12 cm. Alas gelas dibuat dari kain flanel. Jika Ibu membuat 1 lusin alas gelas. Hitunglah keseluruhan luas alas gelas tersebut!
Pembahasan:
Diketahui:
d = 12 cm, r = 6 cm
Jumlah alas gelas = 1 lusin = 12 buah
Ditanya: keseluruhan luas alas gelas?
Jawab:
L = π x r²
L = 3,14 x 6 x 6
L = 113,04 cm²
L keseluruhan alas gelas = 113,04 cm² x 12 = 1356,48 cm²
Jadi, luas keseluruhan alas gelas adalah 1356,48 cm²
13. Sebuah roda sepeda memiliki jari-jari 35 cm. Ketika sepeda dikayuh, roda tersebut berputar sebanyak 50 kali. Jarak yang ditempuh oleh sepeda tersebut?
Baca Juga : Rumus Persegi
Pembahasan:
Diketahui:
r = 35 cm, d = 70 cm
Ditanya: keliling dan jarak tempuh?
Jawab:
K = π x d
K = 22/7 x 70
K = 220 cm
Jarak tempuh = Keliling lingkaran x banyaknya putaran
Jarak tempuh = 220 cm x 50 = 11.000 cm = 110 meter
Jadi, jarak yang ditempuh oleh sepeda adalah 110 meter.
14. Perhatikan gambar berikut ini!
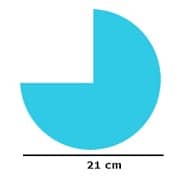
Tentukan Keliling bangun tersebut!
Pembahasan:
Diketahui:
diameter = 21 cm
Ditanya: keliling?
Jawab:
K = π x d
Keliling bangun = garis lengkung + r + r
Keliling bangun = (3/4 x π x d) + r + r
Keliling bangun = (3/4 x 22/7 x 21) + 10,5 + 10,5
Keliling bangun = 70,5 cm
15. Perhatikan Gambar Dibawah ini!
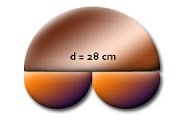
Tentukan keliling dan luas bangun diatas!
Pembahasan:
Diketahui:
diameter 1/2 lingkaran besar = 28 cm
diameter 1/2 lingkaran kecil = 14 cm
Ditanya: keliling dan luas?
Jawab:
a. Keliling Bangun
K = π x d
K 1/2 lingkaran besar = 1/2 x π x d
K 1/2 lingkaran besar = 1/2 x 22/7 x 28
K 1/2 lingkaran besar = 44 cm
K 1/2 lingkaran kecil = 1/2 x π x d
K 1/2 lingkaran kecil = 1/2 x 22/7 x 14
K 1/2 lingkaran kecil = 22 cm
1/2 keliling lingkaran adalah garis lengkung
Keliling bangun = 1/2 K. lingkaran besar + (2 x 1/2 K. lingkaran kecil)
Keliling bangun = 44 cm + (2 x 22 cm ) = 88 cm
Jadi, keliling bangun tersebut adalah 88 cm
b. Luas Bangun
Diketahui:
r lingkaran besar = 14 cm
r lingkaran kecil = 7 cm
Ditanya: luas bangun?
Jawab:
L = π x r²
L 1/2 lingkaran besar = 1/2 x π x r²
L 1/2 lingkaran besar = 1/2 x 22/7 x 14 x 14
L 1/2 lingkaran besar = 308 cm²
L 1/2 lingkaran kecil= 1/2 x π x r²
L 1/2 lingkaran kecil = 1/2 x 22/7 x 7 x 7
L 1/2 lingkaran kecil = 77 cm²
Luas bangun = L.lingkaran besar + (2 x L.lingkaran kecil)
Luas bangun = 308 cm² + (2 x 77 cm²)
Luas bangun = 308 cm² + 154 cm²
Luas bangun = 462 cm²
Jadi, luas bangun di atas adalah 462 cm²
Baca Juga : Rumus Belah Ketupat
Demikian artikel pembahasan tentang pengertian lingkaran, sifat, unsur, rumus, contoh soal lingkaran dan pembahasannya secara lengkap. Semoga bermanfaat
Originally posted 2024-01-11 14:08:35.