Soal Dan Pembahasan Fungsi Komposisi, Aljabar Fungsi dan Komposisi Fungsi Lengkap dengan Cara Penyelesaiannya
Pembahasan tentang Fungsi Komposisi, Aljabar Fungsi Dan Komposisi Fungsi Matematika Disertai Rumus Soal sudah kita bahas pada postingan sebelumnya. Kali ini kita akan bahas bersama-sama soal materi komposisi lengkap dengan cara penyelesaiannya dan contoh latihan soal.
Pembahasan Soal!
Nomor 1
Diketahui fungsi f : R → R dan g : R → R dengan rumus f(x) = x + 1 dan![]()
Tentukan :
a. Daerah asal g(x)
b. Rumus fungsi (fₒg)(x)
c. Rumus fungsi (gₒf)(x)
Penyelesaian
a.
![]()
agar bernilai real, x + 1 ≠ 0 atau x + 5 ≠ 0.
x + 1 ≠ 0 → -1
x + 5 ≠ 0 → -5
Jadi, daerah asal g (x) adalah {x | x ≠ -5, x ≠ -1, x € R}.
b.
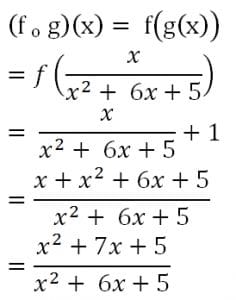
Jadi, rumus fungsi ![]()
c.
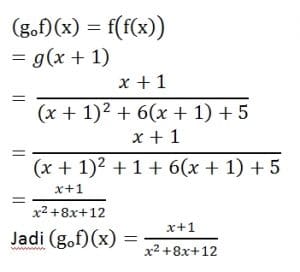
Nomor 2.
Jika f(x)= x2 – 2x + 2 dan g (x) = x + 1 , tentukan :
a. Rumus fungsi (f ₒ g) (x)
b. Nilai a agar (g ₒ f) (a) = 2
Penyelesaian
a. (f ₒ g) (x) = (f (g) (x))
= f ( x + 1 )
= (x + 1)2 – 2(x+1) + 2
= x2 + 2x + 1 – 2x – 2 + 2
= x2 + 1
Jadi, rumus fungsi (f ₒ g) (x) = x2 + 1
b. (g ₒ f)(x) = g(f(x))
= g (x2 – 2x + 2)
= x2 – 2x + 2 + 1
= x2 – 2x + 3
(g ₒ f) (a) = 2
→ a2 – 2a + 3 = 2
→ a2 – 2a + 1 = 0
→ (a – 1)2 = 0
→ a – 1 = 0
→ a = 1
Jadi, nilai a = 1
Nomor 3.
Diketahui ( f ₒ g) (x + 2) = 12x – 5 dan f (x) = 6x + 1. Tentukan
a. g (x)
b. (g ₒ f) (x – 1)
Jawaban
a. Misalkan x + 2 = t → x = t – 2
(g ₒ f) (x + 1) = 12x – 5
→ (f ₒ g) (t) = 12 (t – 2) – 5
→ (f ₒ g) (t) = 12t – 24 – 5
→ (f ₒ g) (t) = 12t – 29
→ (f ₒ g) (t) = 12x – 29
(f ₒ g)(x) = f(g)(x))
→12x – 29 = 6g(x) + 1
→ 6g(x) = 12x – 30
→ g(x) = 2x – 5
Jadi, g(x) = 2x – 5
b. (g ₒ f) (x) = g (f(x))
= g (6x +1)
= 2 (6x + 1) – 5
= 12x – 3
(g ₒ f) (x – 1) = 12 (x – 1) – 3
= 12x – 15
Jadi, (g ₒ f) (x – 1) = 12x – 15
Nomor 4.
Diketahui f(x) = 5x – 3 dan g (x – 2) = 2x + 3. Tentukan :
a. Rumus fungsi g (x)
b. h (x) jika diketahui (h ₒ g) (x) = 6x + 23
jawaban
a. Misalkan t = x – 2 → x = t + 2
g (x – 2) = 2x + 3
→ g (t) = 2 (t + 2) + 3
→ g (t) = 2t + 4 + 3
→ g (t) = 2t + 7
→ g (x) = 2x + 7
Jadi, rumus fungsi g (x) = 2x + 7
b. Misalkan g(x) = t = 2x + 7 → t-7/2
(h ₒ g)(x) = 6x + 23
→ h (g(x)) = 6x + 23
→h(2x + 7) = 6x + 23
→ h (t) = 6 (t-7/2) + 23
→ h (t) = 3 (t – 7) + 23
→ h (t) = 3t + 2
→ h (x) = 3x + 2
Jadi, h (x) = 3x + 2
Latihan soal!
Tentukan bentuk fungsi asal.
Diketahui f (x+1) = 4x + 1 dan (f ₒ g) (x) = 12x – 23 . Dapatkah kamu menentukan f(x) dan g (x)? ikuti dan lengkapilah cara berikut.
1. Misalkan t = x + 1 sehingga x = …. – 1
F (x + 1) = 4x + 1
→ f (t) = 4 (t – … ) + 1
→ f (t) = 4 t – … + 1
→ f (t) = 4t – …
Dengan mengganti t pada f(t) = 4t – 3 dengan x, diperoleh f(x) = 4x – 3. Jadi, f(x) = 4x – 3.
2. (f ₒ g) (x) = 12x – 23
→ f (g(x)) = 12x – 23
→ 4g (x) – 3 = 12x – 23
→4g (x) = 12x – 23 + ….
→ 4g (x) = 12x – ….
→ g (x) = 3x – 5
Jadi, g(x) = 3x -5.
Dengan diberikannya materi pembahasan soal tentang fungsi komposisi, diharapakan dapat membantu dan menambah wawasan para pembaca khusus nya dalam materi komposisi. Semoga artikel ini bermanfaat, samapi bertemu dipostingan selanjutnya…