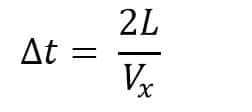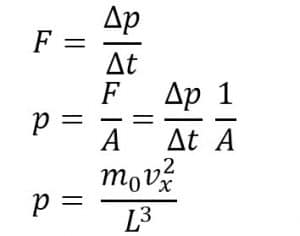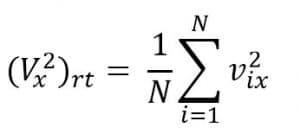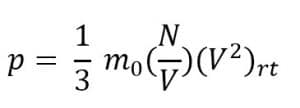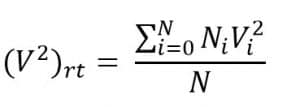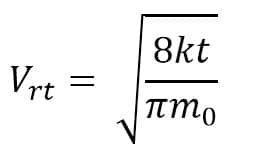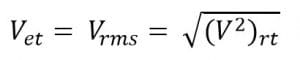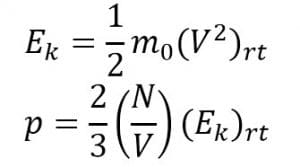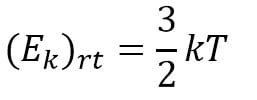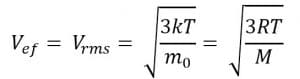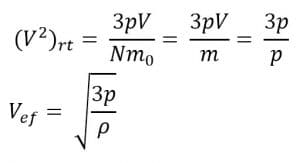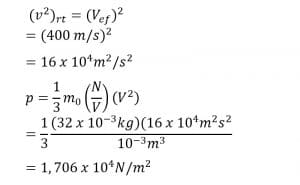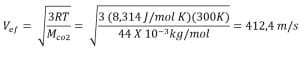Teori Kinetik Gas - Teorema Ekuipartisi Energi Dan Hubungan Antara Tekanan, Suhu Dan Energi Partikel Gas

Melanjutkan postingan sebelumnya tentang Persamaan Umum Gas, Hukum Gas Ideal Dan Pembahasan Contoh Soal, pada postingan tersebut kita telah membahasa tentang persamaan umum gas, dan hukum dari persamaan keadaan gas yang dilengkapi dengan rumus masing-masing dan pembahasan contoh soal nya. Namun pada teori kinetik gas terdapat juga jenis lainnya antara lain teorema ekuipartisi energi dan Tekanan, suhu dan energi Gas yang akan kita pelajari dibawah ini.

Contents hide

1 Teorema Ekuipartisi Energi

1.1 Contoh Soal !

2 Tekanan, Suhu, dan Energi Gas

2.1 Contoh soal!

2.2 Baca postingan selanjutnya:

Teorema Ekuipartisi Energi

1. Hubungan Energi Kinetik Tiap Sumbu dengan Energi Kinetik Keseluruhan

Energi kinetik pada salah satu sumbu, perumusannya sebagai berikut.

(E_kx)_rt = (E_ky)_rt = (E_kz) = ⅓ (E_k)_rt

2. Derajat Kebebasan (Degree of Freedom) Gas Monoatomik

Derajat kebebasan adalah kemampuan molekul untuk berperan dalam suatu gerakan satu dimensi yang memberi sumbangan ke energi mekanik molekul, disingkat df.

Energi mekanik dapat dirumuskan:

(E_m)_rt = (E_k)_rt= df (½ kT) = 3(½ kT)

3. Derajat Kebebasan Gas Diatomik

Gas diatomik dapat melakukan geraktranslasi, vibrasi, dan rotasi. Derajat kebebasan gas diatomik:

pada suhu rendah (± 250 K) = 3
pada suhu sedang (± 500 K) = 5
pada suhu tinggi (± 1.000 K) = 7

4. Energi Dakhil (Internal Energy) Gas

Energi dakhil atau energi internal biasa disebut dengan energi dalam, perumusannya:

Dengan U = energy internal

Contoh Soal !

1. Sebuah gas memiliki energi kinetik rata-rata total 9 x 10^-21 joule. Berapakah energi kinetik pada sumbu X?

Penyelesaian:

Diketahui: (E_k)_rt = 9×10^-21 joule
Ditanyakan: E_kx

Jawab:

Energi kinetik pada sumbu X adalah sepertiga dari energi kinetik rata-rata total.

E_kx = ⅓ (E_kx)_rt

= ⅓ (9 x 10^-21 joule) = 3 x 10^-21 joule

Jadi, energy kinetic pada sumbu X sebesar 3 x 10^-21 joule

2. Dua mol gas diatomik mempunyai energi kinetik 7 x 10^-20 joule. Berapakah energi dalamnya?

Penyelesaian:

Diketahui :
n = 2 mol
(E_kx)_rt = 7 x 10^-20 joule

Ditanyakan :U

Jawab:

N = n N_A

= (2mol )(6,02 x 10²³ molekul/mol)

= 12,04 x 10²³ molekul

U = N (E_kx)_rt

= (12,04 x 10²³) (7 x 10^-20 joule)

= 84,28 x 10³ joule = 84,28 kJ

Jadi, gas diamomik tersebut mempunyai energy dalam sebesar 84,28 kJ.

Tekanan, Suhu, dan Energi Gas

1. Model Partikel Gas

Sifat-sifat gas dapat dijelaskan dengan dasar sebagai berikut.

Gas terdiri atas molekul dalam jumlah besar.
Partikel-partikel gas bergerak dalam lintasan lurus dengan kelajuan tetap dan geraknya acak karena v tumbukan.
Semua tumbukan bersifat lenting sempurna.
Selang waktu tumbukan antarpartikel sangat sedikit.
Volume partikel gas sangat kecil dibandingkan dengan volume ruang yang ditempati, sehingga dapat diabaikan.
Pada semua partikel gas berlaku hukum Newton tentang gerak.

2. Hubungan Antara Tekanan, Suhu, dan Energi Partikel Gas

a. Tekanan sebagai Fungsi Kecepatan Rata-Rata

Sebuah molekul gas bermassa m₀ berada pada kubus dengan rusuk L leluasa bergerak ke segala arah. Kecepatan molekul dapat dirumuskan:

V = v_x i + v_y j + v_z k

Komponen momentum pada sumbu X setelah tumbukan:

Px = m₀ V_x = -m₀V_x

Tanda negatif muncul karena perubahan arah setelah tumbukan. Perubahan momentum setelah tumbukan adalah:

∆p = 2m₀V_x

Waktu yang dibutuhkan untuk menempuh dinding satu ke dinding lain:

Menurut hukum II Newton

Jika ada sejumlah N molekul gas dalam ruang tertutup, kelajuan kuadrat rata-rata pada arah x:

Tekanan dapat dinyatakan dalam kelajuan rata-rata menjadi seperti berikut.

Keterangan:
p = tekanan (N/m²)
m₀ = massa partake; (kg)
N = jumlah partikel
V = volume ruangan (m³)
(v²)_rt = kelajuan kuadrat rata-rata (m/s)

b. Kelajuan Rata-Rata, Kelajuan Kuadrat Rata-Rata, dan Kelajuan Efektif

Kelajuan Rata-Rata

Jika dalam suatu ruang terdapat N molekul dengan kelajuan berbeda, kelajuan rata-ratanya:

Berdasarkan distribusi Maxwell-Boltzman, akan didapatkan persamaan:

Kelajuan Kuadrat Rata-Rata

Kelajuan kuadrat rata-rata dapat dirumuskan

Kelajuan Efektif (Kelajuan rms) Besarnya kelajuan efektif dapat ditulis

c. Hubungan Antara Tekanan Gas dengan Energi Kinetik Rata-Rata

Energi kinetik berhubungan dengan kelajuan kuadrat rata-rata dan tekanan. Perumusannya sebagai berikut:

Keterangan:
p = tekanan (N/m²)
N = jumalh partikel
V = volume ruangan (m³)
(E_k)_rt= energy kinetic rata-rata (J)

d. Hubungan Temperatur dengan Energi Kinetik Gas

Hubungan antara energi kinetik dengan suhu adalah:

Keterangan :
(E_k)_rt= energy kinetic rata-rata (J)
K = tetapan Boltzman (1,38 x 10^-23J/K)

e. Hubungan Antara Temperatur dengan Kelajuan Efektif Gas

Kelajuan efektif dapat dirumuskan sebagai berikut.

Keterangan:
V_ef = kelajuan efektif (m/s)
m₀ = massa partikel (kg)
M = massa atom gas (kg/mol)
R = tetapan umum gas (8,134 J/mol K)

f. Hubungan Antara Tekanan dengan Kelajuan Efektif

Contoh soal!

1. Satu mol gas O₂ berada dalam tangki 1 liter. Apabila laju efektif gas oksigen 400 m/s, berapakah tekanan partikel dalam wadah tersebut.?

Penyelesaian:

Diketahui:
No₂ = 1 mol
Vo₂ = 10^-3 m³V_ef = 400 m/s

Ditanyakan : p

Jawab:

N m₀ = n Mo₂

= (1 mol) (32 g/mol)

= 32 g

= 32 x 10^-3 kg

Jadi, partikel dalam wadah sebesar 1, 706 x 10⁴ N/m²

2. Tentukan kelajuan efektif 1 mol gas CO₂ pada suhu 27°C!

Penyelesaian :

Diketahui:
M_co2 = 44 g/mol = 44 x 10^-3 kg/mol
T = 27 + 273 = 300 K

Ditanyakan : V_ef

Jawab:

Jadi, kelajuan efektif 1 mol gas CO₂ sebesar 412,4 m/s

Demikian penjelasan yang bisa kami sampaikan tentang Teori Kinetik Gas – Teorema Ekuipartisi Energi Dan Hubungan Antara Tekanan, Suhu Dan Energi Partikel Gas. Semoga postingan ini bermanfaat bagi pembaca dan bisa dijadikan sumber literatur untuk mengerjakan tugas. Sampai jumpa pada postingan selanjutnya.